ńźŠĽÉ gi√ļp c√°c em hŠĽćc sinh c√≥ th√™m t√†i liŠĽáu hŠĽćc tŠļ≠p, r√®n luyŠĽán chuŠļ©n bŠĽč cho k√¨ thi HK1 lŠĽõp 10 sŠļĮp tŠĽõi, HŠĽĆC247 ńĎ√£ bi√™n soŠļ°n, tŠĽēng hŠĽ£p nŠĽôi dung t√†i liŠĽáu ńź√™ŐÄ thi HK1 m√īn ToaŐĀn 10 CTST nńÉm 2023 - 2024 coŐĀ ńĎaŐĀp aŐĀn tr∆į∆°ŐÄng THPT Thanh HaŐÄ gi√ļp c√°c em hŠĽćc tŠļ≠p r√®n luyŠĽán tŠĽĎt h∆°n. Hi vŠĽćng ńĎ√Ęy l√† t√†i liŠĽáu hŠĽĮu √≠ch cho c√°c em trong qu√° tr√¨nh hŠĽćc tŠļ≠p v√† √īn thi ToaŐĀn 10 Ch√Ęn tr∆°ŐÄi saŐĀng taŐ£o. Ch√ļc c√°c em thi tŠĽĎt!
1. ńź√™ŐÄ thi
|
S∆°ŐČ GD & ńźT HaŐČi D∆į∆°ng Tr∆į∆°ŐÄng THPT Thanh HaŐÄ
|
ńź√™ŐÄ ki√™ŐČm tra HoŐ£c kiŐÄ 1 NńÉm hoŐ£c: 2023 ‚Äď 2024 M√īn: ToaŐĀn 10 ‚Äď Ch√Ęn tr∆°ŐÄi saŐĀng taŐ£o Th∆°ŐÄi gian: 90p (Kh√īng k√™ŐČ th∆°ŐÄi gian phaŐĀt ńĎ√™ŐÄ) |
I. PHŠļ¶N TRŠļģC NGHIŠĽÜM (7.0 ńĎiŠĽÉm).
C√Ęu 1. Cho tŠļ≠p hŠĽ£p \(A=\left\{ 1;2;3 \right\}\). TŠļ≠p hŠĽ£p n√†o sau ńĎ√Ęy kh√īng phŠļ£i l√† tŠļ≠p con cŠĽßa tŠļ≠p A?
A. \(\left\{ 2;3;4 \right\}\). B. \(\varnothing \).
C. A. D. \(\left\{ 1;2 \right\}\).
C√Ęu 2. Cho tŠļ≠p hŠĽ£p \(A=\left\{ 1;2;3 \right\}\) v√† \(B=\left\{ 2;4 \right\}\). T√¨m tŠļ≠p hŠĽ£p \(A\backslash B\).
A. \(A\backslash B=\left\{ 1;4 \right\}\). B. \(A\backslash B=\left\{ 1;3 \right\}\).
C. \(A\backslash B=\left\{ 2 \right\}\). D. \(A\backslash B=\left\{ 4 \right\}\).
C√Ęu 3. BŠļ•t ph∆į∆°ng tr√¨nh n√†o sau ńĎ√Ęy l√† bŠļ•t ph∆į∆°ng tr√¨nh bŠļ≠c nhŠļ•t hai Šļ©n?
A. \(2{{x}^{2}}-3y<0\). B. \(-x+4y>-3\).
C. \(x+{{y}^{2}}\ge 2\). D. \({{x}^{2}}+4{{y}^{2}}\le 6\).
C√Ęu 4. Trong c√°c hŠĽá sau, hŠĽá n√†o kh√īng phŠļ£i l√† hŠĽá bŠļ•t ph∆į∆°ng tr√¨nh bŠļ≠c nhŠļ•t hai Šļ©n?
A. \(\left\{ \begin{align} & x+y>0 \\ & x>1 \\ \end{align} \right.. \)
B. \(\left\{ \begin{align} & x+y=-2 \\ & x-y=5 \\ \end{align} \right..\)
C. \(\left\{ \begin{align} & 2x+3y>10 \\ & x-4y<1 \\ \end{align} \right.. \)
D. \(\left\{ \begin{align} & y>0 \\ & x-4\le 1 \\ \end{align} \right..\)
C√Ęu 5. PhŠļßn kh√īng gŠļ°ch ch√©o ŠĽü h√¨nh sau ńĎ√Ęy (kh√īng t√≠nh bŠĽĚ) l√† biŠĽÉu diŠĽÖn miŠĽĀn nghiŠĽám cŠĽßa hŠĽá bŠļ•t ph∆į∆°ng tr√¨nh n√†o trong bŠĽĎn hŠĽá A, B, C, D?

A. \(\left\{ \begin{align} & y>0 \\ & 3x+2y<6 \\ \end{align} \right.. \)
B. \( \left\{ \begin{align} & y>0 \\ & 3x+2y<-6 \\ \end{align} \right.. \)
C. \(\left\{ \begin{align} & x>0 \\ & 3x+2y<6 \\ \end{align} \right.. \)
D. \(\left\{ \begin{align} & x>0 \\ & 3x+2y>-6 \\ \end{align} \right..\)
C√Ęu 6. Trong c√°c ńĎŠļ≥ng thŠĽ©c sau ńĎ√Ęy, ńĎŠļ≥ng thŠĽ©c n√†o ńĎ√ļng?
A. \(\sin 120{}^\circ =\frac{\sqrt{3}}{2}\).
B. \(\cos 120{}^\circ =\frac{1}{2}\).
C. \(\tan 120{}^\circ =\sqrt{3}\).
D. \(\cot 120{}^\circ =-\sqrt{3}\).
C√Ęu 7. Trong c√°c khŠļ≥ng ńĎŠĽčnh sau, khŠļ≥ng ńĎŠĽčnh n√†o sai?
A. \(\cos {{60}^{\text{o}}}=\sin {{30}^{\text{o}}}\).
B. \(\cos {{60}^{\text{o}}}=\sin {{120}^{\text{o}}}\).
C. \(\cos {{60}^{\text{o}}}=-\cos {{120}^{\text{o}}}\).
D. \(\sin {{60}^{\text{o}}}=\cos {{30}^{\text{o}}}\).
C√Ęu 8. ChŠĽćn c√īng thŠĽ©c ńĎ√ļng trong c√°c c√īng thŠĽ©c sau
A. \(S=\frac{1}{2}bc\sin B\,.\)
B. \(S=\frac{1}{2}bc\sin A\,.\)
C. \(S=\frac{1}{2}ab\sin B\,.\)
D. \(S=\frac{1}{2}ac\sin C\,.\)
C√Ęu 9.Tam gi√°c ABC vu√īng tŠļ°i A c√≥ \(BC=8\sqrt{3}\,\text{cm}\). T√≠nh b√°n k√≠nh R cŠĽßa ńĎ∆įŠĽĚng tr√≤n ngoŠļ°i tiŠļŅp tam gi√°c ABC.
A. \(R=16\sqrt{3}\,\text{cm}\).
B. \(R=2\sqrt{3}\,\text{cm}\).
C. \(R=4\sqrt{3}\,\text{cm}\).
D. \(R=8\sqrt{3}\,\text{cm}\).
C√Ęu 10. Cho ba ńĎiŠĽÉm A,B,C thŠļ≥ng h√†ng v√† B ŠĽü giŠĽĮa nh∆į h√¨nh vŠļĹ sau.
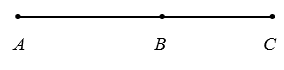
CŠļ∑p vect∆° n√†o sau ńĎ√Ęy c√Ļng h∆įŠĽõng?
A. \(\overrightarrow{BC}\) và \(\overrightarrow{BA}\).
B. \(\overrightarrow{CB}\) và \(\overrightarrow{AC}\).
C. \(\overrightarrow{CB}\) và \(\overrightarrow{AB}\).
D. \(\overrightarrow{BC}\) và \(\overrightarrow{AB}\).
C√Ęu 11. TŠĽēng \(\overrightarrow{MN}+\overrightarrow{NE}+\overrightarrow{EM}\) bŠļĪng
A. \(\overrightarrow{0}\).
B. \(\overrightarrow{ME}\).
C. \(\overrightarrow{MP}\).
D. 0.
C√Ęu 12. Cho ba ńĎi√™ŐČm A, B, C. M√™Ő£nh ńĎ√™ŐÄ naŐÄo sau ńĎ√Ęy laŐÄ ńĎuŐĀng?
A. \(\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\).
B. \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{BC}\).
C. \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}\).
D. \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{BC}\).
C√Ęu 13. Cho ńĎoŠļ°n thŠļ≥ng \(AB\). GŠĽći \(M\) l√† mŠĽôt ńĎiŠĽÉm tr√™n ńĎoŠļ°n thŠļ≥ng \(AB\) sao cho \(AM=\frac{1}{3}AB\). KhŠļ≥ng ńĎŠĽčnh n√†o sau ńĎ√Ęy ńĎ√ļng?
A. \(\overrightarrow{MA}=\frac{1}{3}\overrightarrow{MB}\).
B. \(\overrightarrow{AM}=\frac{1}{3}\overrightarrow{MB}\).
C. \(\overrightarrow{BM}=2\overrightarrow{MA}\).
D. \(\overrightarrow{MB}=2\overrightarrow{MA}\).
C√Ęu 14. Cho \(\overrightarrow{a}=-2\overrightarrow{b}\). KhŠļ≥ng ńĎŠĽčnh ńĎ√ļng l√†
A. \(\overrightarrow{a} v√† \overrightarrow{b}\) c√Ļng h∆įŠĽõng.
B. \(\overrightarrow{a} và \overrightarrow{b}\) có giá song song.
C. \(\overrightarrow{a} v√† \overrightarrow{b}\) ng∆įŠĽ£c h∆įŠĽõng v√† \(\left| \overrightarrow{a} \right|=2\left| \overrightarrow{b} \right|\).
D. \(\overrightarrow{a} v√† \overrightarrow{b}\) ng∆įŠĽ£c h∆įŠĽõng v√† \(\left| \overrightarrow{a} \right|=-2\left| \overrightarrow{b} \right|\).
C√Ęu 15. Cho h√¨nh vu√īng ABCD cŠļ°nh bŠļĪng a. Khi ńĎ√≥ \(\left| \overrightarrow{AB}+\overrightarrow{AD} \right|\) bŠļĪng
A. 2a. B. a. C. \(a\sqrt{2}\). D. \(\frac{a\sqrt{3}}{2}\).
C√Ęu 16. H√£y chŠĽćn kŠļŅt quŠļ£ ńĎ√ļng khi ph√Ęn t√≠ch vect∆° \(\overrightarrow{AM}\) theo hai v√©ct∆°\(\overrightarrow{AB}\) v√† \(\overrightarrow{AC}\) cŠĽßa tam gi√°c ABC vŠĽõi trung tuyŠļŅn AM.
A. \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}.\)
B. \(\overrightarrow{AM}=2\overrightarrow{AB}+3\overrightarrow{AC}.\)
C. \(\overrightarrow{AM}=\frac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right).\)
D. \(\overrightarrow{AM}=\frac{1}{3}\left( \overrightarrow{AB}+\overrightarrow{AC} \right).\)
C√Ęu 17. Trong mŠļ∑t phŠļ≥ng tŠĽća ńĎŠĽô Oxy, cho \(A\left( 5;3 \right), B\left( 7;8 \right)\). T√¨m tŠĽća ńĎŠĽô cŠĽßa vect∆° \(\overrightarrow{AB}\).
A. \(\left( 12;11 \right)\). B. \(\left( 2;5 \right)\).
C. \(\left( 2;6 \right)\). D. \(\left( -2;-5 \right)\).
C√Ęu 18. Trong mŠļ∑t phŠļ≥ng tŠĽća ńĎŠĽô \(Oxy\), cho \(\overrightarrow{a}=\left( -1;\,1 \right),\,\overrightarrow{b}=\left( 4;\,-2 \right)\). TŠĽća ńĎŠĽô cŠĽßa \(\overrightarrow{u}=\overrightarrow{2a}+\overrightarrow{b}\) l√†
A. \(\left( 6;\,0 \right).\) B. \(\left( 3;\,-1 \right).\)
C. \(\left( 2;\,0 \right).\) D. \(\left( 7;\,-3 \right).\)
C√Ęu 19. Trong mŠļ∑t phŠļ≥ng vŠĽõi hŠĽá trŠĽ•c tŠĽća ńĎŠĽô \(Oxy\), cho hai ńĎiŠĽÉm \(M\left( -3;1 \right)\) v√† \(N\left( 6;-4 \right)\). TŠĽća ńĎŠĽô trŠĽćng t√Ęm \(G\) cŠĽßa tam gi√°c OMN l√†
A. \(G\left( 9;-5 \right).\) B. \(G\left( -1;1 \right).\)
C. \(G\left( 1;-1 \right).\) D. \(G\left( 3;-3 \right).\)
C√Ęu 20. Trong mŠļ∑t phŠļ≥ng toŠļ° ńĎŠĽô \(Oxy\),khoŠļ£ng c√°ch giŠĽĮa hai ńĎiŠĽÉm \(A\left( 1;4 \right)\) v√† \(B\left( 3;2 \right)\) l√†
A. 4. B. \(2\sqrt{2}\). C. 8. D. 2.
---(ńźŠĽÉ xem tiŠļŅp nŠĽôi dung trńÉŐĀc nghi√™Ő£m cŠĽßa ńĎ√™ŐÄ thi c√°c em vui l√≤ng xem tŠļ°i online hoŠļ∑c ńĎńÉng nhŠļ≠p v√†o HŠĽĆC247 ńĎŠĽÉ tŠļ£i vŠĽĀ m√°y)---
2. ńźaŐĀp aŐĀn
|
1. A |
2. B |
3. B |
4. B |
5. A |
6. A |
7. B |
8. B |
9. C |
10. D |
|
11. A |
12. A |
13. C |
14. C |
15. C |
16. C |
17. B |
18. C |
19. C |
20. B |
|
21. A |
22. A |
23. D |
24. A |
25. C |
26. A |
27. C |
28. D |
29. D |
30. B |
|
31. D |
32. D |
33. C |
34. A |
35. A |
|
|
|
|
|
Tr√™n ńĎ√Ęy l√† mŠĽôt phŠļßn tr√≠ch ńĎoŠļ°n nŠĽôi dung ńź√™ŐÄ thi HK1 m√īn ToaŐĀn 10 CTST nńÉm 2023 - 2024 coŐĀ ńĎaŐĀp aŐĀn tr∆į∆°ŐÄng THPT Thanh HaŐÄ. ńźŠĽÉ xem to√†n bŠĽô nŠĽôi dung c√°c em chŠĽćn chŠĽ©c nńÉng xem online hoŠļ∑c ńĎńÉng nhŠļ≠p v√†o trang hoc247.net ńĎŠĽÉ tŠļ£i t√†i liŠĽáu vŠĽĀ m√°y t√≠nh.
MŠĽĚi c√°c em tham khŠļ£o t√†i liŠĽáu c√≥ li√™n quan:
Hy vŠĽćng bŠĽô ńĎŠĽĀ thi n√†y sŠļĹ gi√ļp c√°c em hŠĽćc sinh √īn tŠļ≠p tŠĽĎt v√† ńĎŠļ°t th√†nh t√≠ch cao trong k√¨ thi sŠļĮp tŠĽõi.
T√†i liŠĽáu li√™n quan
T∆į liŠĽáu nŠĽēi bŠļ≠t tuŠļßn
-
ńźŠĽĀ thi minh hŠĽća m√īn To√°n tŠĽĎt nghiŠĽáp THPT nńÉm 2025
22/10/20241300 - Xem thêm





