NhαΚ±m giΟΚp cΟΓc em hαΜçc sinh cΟ≥ thΟΣm tΟ†i liαΜ΅u hαΜçc tαΚ≠p, rΟ®n luyαΜ΅n chuαΚ©n bαΜ΄ cho kΟ§ thi giαΜ·a HK1 mΟ¥n ToΟΓn 10 sαΚ·p tαΜ¦i, HαΜ¨C247 ΡëΟΘ biΟΣn soαΚΓn, tαΜïng hαΜΘp nαΜôi dung tΟ†i liαΜ΅u ΡêαΜ¹ thi giαΜ·a HK1 mΟ¥n ToΟΓn 10 CTST nΡÉm hoΧΘc 2023 - 2024 TrΤΑΤΓΧÄng THPT TΤΑΧ¹ KiΟΣΧΘt coΧ¹ ΡëaΧ¹p aΧ¹n giΟΚp cΟΓc em hαΜçc tαΚ≠p rΟ®n luyαΜ΅n tαΜët hΤΓn. Hi vαΜçng ΡëαΜ¹ thi dΤΑαΜ¦i ΡëΟΔy lΟ† tΟ†i liαΜ΅u hαΜ·u Ο≠ch cho cΟΓc em trong quΟΓ trΟ§nh hαΜçc tαΚ≠p vΟ† Ο¥n thi. ChΟΚc cΟΓc em thi tαΜët!
1. ΡêΟΣΧÄ thi
|
SΤΓΧâ giaΧ¹o duΧΘc vaΧÄ ΡëaΧÄo taΧΘo TiΟΣΧÄn Giang TrΤΑΤΓΧÄng THPT TΤΑΧ¹ KiΟΣΧΘt |
ΡêΟäΧÄ KIΟäΧâM TRA GIΤ·ΧÉA HOΧΘC KIΧÄ 1 NΡÉm hoΧΘc: 2023 βÄ™ 2024 MΟ¥n: ToaΧ¹n 10 βÄ™ CTST ThΤΓΧÄi gian: 90p |
A. TRαΚ°C NGHIαΜÜM (7,0 ΡëiαΜÉm)
CΟΔu 1: BαΚΞt phΤΑΤΓng trΟ§nh nΟ†o sau ΡëΟΔy lΟ† bαΚΞt phΤΑΤΓng trΟ§nh bαΚ≠c nhαΚΞt hai αΚ©n?
A. \(2{{x}^{2}}-3y<0\). B. \(x+{{y}^{2}}\ge 2\). C. \({{x}^{2}}+4{{y}^{2}}\le 6\). D. \(-x+4y>-3\).
CΟΔu 2: Trong cΟΓc ΡëαΚ≥ng thαΜ©c sau ΡëΟΔy ΡëαΚ≥ng thαΜ©c nΟ†o lΟ† ΡëΟΚng?
A. \(\text{cot}{{150}^{\circ }}=\sqrt{3}\). B. \(\text{tan}{{150}^{\circ }}=-\frac{1}{\sqrt{3}}\).
C. \(\text{sin}{{150}^{\circ }}=-\frac{\sqrt{3}}{2}\). D. \(\text{cos}{{150}^{\circ }}=\frac{\sqrt{3}}{2}\).
CΟΔu 3: XΟ©t mαΜ΅nh ΡëαΜ¹ chαΜ©a biαΚΩn: \(P\left( x \right)\): " x lΟ† sαΜë nguyΟΣn tαΜë". Trong cΟΓc mαΜ΅nh ΡëαΜ¹ sau, mαΜ΅nh ΡëαΜ¹ nΟ†o ΡëΟΚng?
A. \(P\left( 6 \right)\). B. \(P\left( 9 \right)\). C. \(P\left( 13 \right)\) D. \(P\left( 15 \right)\).
CΟΔu 4: MiαΜ¹n nghiαΜ΅m cαΜßa bαΚΞt phΤΑΤΓng trΟ§nh \(x+y\le 2\) lΟ† phαΚßn tΟ¥ ΡëαΚ≠m trong hΟ§nh vαΚΫ cαΜßa hΟ§nh vαΚΫ nΟ†o, trong cΟΓc hΟ§nh vαΚΫ sau?
A. 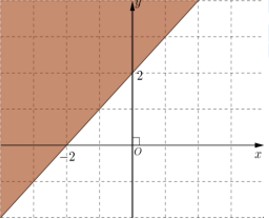
B. 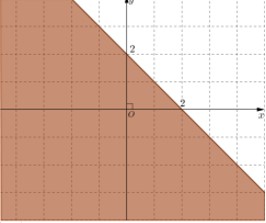
C. 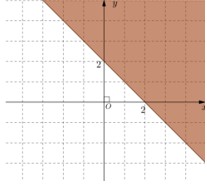
D. 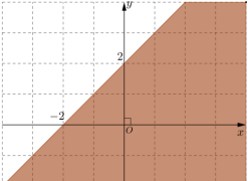
CΟΔu 5: Cho \(A=\left[ -3;2 \right)\). TαΚ≠p hαΜΘp \({{C}_{\mathbb{R}}}A\) lΟ†
A. \(\left[ 2;+\infty \right)\) B. \(\left( -\infty ;-3 \right)\)
C. \(\left( 3;+\infty \right)\). D. \(\left( -\infty ;-3 \right)\).
CΟΔu 6: MiαΜ¹n khΟ¥ng bαΜ΄ gαΚΓch trong hΟ§nh bΟΣn ΡëΤΑαΜ¦i lΟ† hΟ§nh biαΜÉu ΡëiΟΣn miαΜ¹n nghiαΜ΅m cαΜßa bαΚΞt phΤΑΤΓng trΟ§nh bαΚ≠c nhαΚΞt nΟ†o sau ΡëΟΔy?
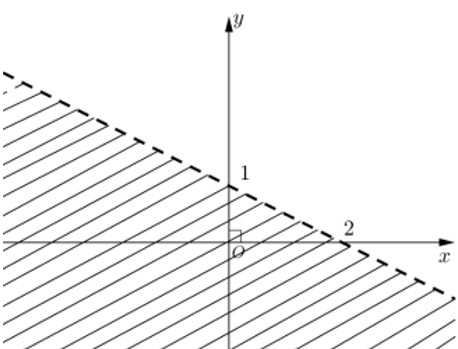
A. \(x+2y-2\ge 0\). B. \(x+2y+1\le 0\).
C. \(x+2y-2>0\). D. \(2x-y+1>0\).
CΟΔu 7: Trong cΟΓc hαΜ΅ bαΚΞt phΤΑΤΓng trΟ§nh sau, hαΜ΅ bαΚΞt phΤΑΤΓng trΟ§nh nΟ†o lΟ† hαΜ΅ bαΚΞt phΤΑΤΓng trΟ§nh bαΚ≠c nhαΚΞt hai αΚ©n?
A. \(\left\{ \begin{array}{*{35}{l}} x-y\le 3 \\ y<1 \\ x+y\ge x+xy \\ \end{array} \right.\)
B. \(\left\{ \begin{array}{*{35}{l}} x>3 \\ y<2 \\ x+y\ge {{y}^{2}} \\ \end{array} \right.\)
C. \( \left\{ \begin{array}{*{35}{l}} 2x+3y>4 \\ {{2}^{3}}x+{{3}^{2}}y<1 \\ \end{array} \right.\)
D. \(\left\{ \begin{array}{*{35}{l}} 2x+3y>4 \\ {{2}^{3}}x+3{{y}^{2}}<1 \\ \end{array} \right.\)
CΟΔu 8: PhΟΓt biαΜÉu nΟ†o sau ΡëΟΔy lΟ† mαΜôt mαΜ΅nh ΡëαΜ¹?
A. SαΜë 3 cΟ≥ phαΚΘi lΟ† sαΜë tαΜ± nhiΟΣn? B. Con Ρëang lΟ†m gΟ§ ΡëΟ≥.
C. New YorklαΚ© thαΜß ΡëΟ¥ cαΜßa ViαΜ΅t Nam. D. TrαΜùi hΟ¥m nay ΡëαΚΙp quΟΓ!
CΟΔu 9: MαΜ΅nh ΡëαΜ¹ βÄ€ \(\exists x\in \mathbb{R},{{x}^{2}}=15\) " ΡëΤΑαΜΘc phΟΓt biαΜÉu lΟ†
A. BΟ§nh phΤΑΤΓng cαΜßa mαΜ½i sαΜë thαΜ±c bαΚ±ng 15 .
B. NαΚΩu x lΟ† mαΜôt sαΜë thαΜ±c thΟ§ \({{x}^{2}}=15\).
C. ChαΜâ cΟ≥ mαΜôt sαΜë thαΜ±c mΟ† bΟ§nh phΤΑΤΓng cαΜßa nΟ≥ bαΚ±ng 15.
D. CΟ≥ Ο≠t nhαΚΞt mαΜôt sαΜë thαΜ±c mΟ† bΟ§nh phΤΑΤΓng cαΜßa nΟ≥ bαΚ±ng 15 .
CΟΔu 10: Cho \(\text{tan}\alpha =2\). GiΟΓ trαΜ΄ cαΜßa \(A=\frac{3\text{sin}\alpha +\text{cos}\alpha }{\text{sin}\alpha -\text{cos}\alpha }\) lΟ†
A. 7 . B. 5 . C. \(\frac{5}{3}\). D. \(\frac{7}{3}\).
CΟΔu 11: Cho mαΜ΅nh ΡëαΜ¹: "NαΚΩu tam giΟΓc cΟ≥ hai gΟ≥c bαΚ±ng \({{60}^{\circ }}\) thΟ§ tam giΟΓc ΡëΟ≥ lΟ† tam giΟΓc ΡëαΜ¹u". MαΜ΅nh ΡëαΜ¹ ΡëαΚΘo cαΜßa mαΜ΅nh ΡëαΜ¹ trΟΣn lΟ†:
A. NαΚΩu tam giΟΓc cΟ≥ hai gΟ≥c bαΚ±ng \({{60}^{\circ }}\) thΟ§ tam giΟΓc ΡëΟ≥ khΟ¥ng lΟ† tam giΟΓc ΡëαΜ¹u.
B. NαΚΩu tam giΟΓc lΟ† tam giΟΓc ΡëαΜ¹u thΟ§ tam giΟΓc ΡëΟ≥ cΟ≥ hai gΟ≥c bαΚ±ng \({{60}^{\circ }}\).
C. Tam giΟΓc lΟ† tam giΟΓc ΡëαΜ¹u nαΚΩu vΟ† chαΜâ nαΚΩu tam giΟΓc ΡëΟ≥ cΟ≥ hai gΟ≥c bαΚ±ng \({{60}^{\circ }}\).
D. NαΚΩu mαΜôt tam giΟΓc lΟ† tam giΟΓc ΡëαΜ¹u thΟ§ tam giΟΓc ΡëΟ≥ cΟ≥ hai gΟ≥c bαΚ±ng nhau.
CΟΔu 12: CΟΓch phΟΓt biαΜÉu nΟ†o khΟ¥ng thαΜÉ dΟΙng ΡëαΜÉ phΟΓt biαΜÉu mαΜ΅nh ΡëαΜ¹ \(A\Rightarrow B\)?
A. A kΟ©o theo B. B. A lΟ† ΡëiαΜ¹u kiαΜ¹n ΡëαΜß ΡëαΜÉ cΟ≥ B.
C. A lΟ† ΡëiαΜ¹u kiαΜ¹n cαΚßn ΡëαΜÉ cΟ≥ B. D. NαΚΩu ~A thΟ§ B.
CΟΔu 13: MiαΜ¹n nghiαΜ΅m cαΜßa bαΚΞt phΤΑΤΓng trΟ§nh \(-3x+y+2\le 0\) khΟ¥ng chαΜ©a ΡëiαΜÉm nΟ†o sau ΡëΟΔy?
A. \(A\left( 1;2 \right)\). B. \(C\left( 1;\frac{1}{2} \right)\).
C. \(D\left( 3;1 \right)\). D. \(B\left( 2;1 \right)\).
CΟΔu 14: Cho tam giΟΓc ABC cΟ≥ \(AB=4\text{ }\!\!~\!\!\text{ cm},BC=7\text{ }\!\!~\!\!\text{ cm},CA=9\text{ }\!\!~\!\!\text{ cm}\). GiΟΓ trαΜ΄ \(\text{cos}A\) lΟ†
A. \(\frac{2}{3}\). B. \(-\frac{2}{3}\). C. \(\frac{1}{3}\). D. \(\frac{1}{2}\).
CΟΔu 15: Trong cΟΓc ΡëαΚ≥ng thαΜ©c sau, ΡëαΚ≥ng thαΜ©c nΟ†o ΡëΟΚng ?
A. \(\text{sin}\left( {{180}^{\circ }}-a \right)=\text{sin}a\).
B. \(\text{sin}\left( {{180}^{\circ }}-a \right)=\text{cos}a\).
C. \(\text{sin}\left( {{180}^{\circ }}-a \right)=-\text{cos}a\).
D. \(\text{sin}\left( {{180}^{\circ }}-a \right)=-\text{sin}a\).
CΟΔu 16: Cho A,B lΟ† hai tαΚ≠p hαΜΘp ΡëΤΑαΜΘc minh hαΜça nhΤΑ hΟ§nh vαΚΫ. PhαΚßn tΟ¥ Ρëen trong hΟ§nh vαΚΫ lΟ† tαΚ≠p hαΜΘp nΟ†o sau ΡëΟΔy?
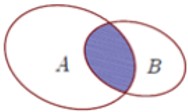
A. \(A\setminus B\). B. \(B\setminus A\). C. \(A\cap B\). D. \(A\cup B\).
CΟΔu 17: Trong hΟ§nh vαΚΫ dΤΑαΜ¦i, phαΚßn mαΚΖt phαΚ≥ng khΟ¥ng bαΜ΄ gαΚΓch sαΜçc (kαΜÉ bαΜù) lΟ† miαΜ¹n nghiαΜ΅m cαΜßa hαΜ΅ bαΚΞt phΤΑΤΓng trΟ§nh
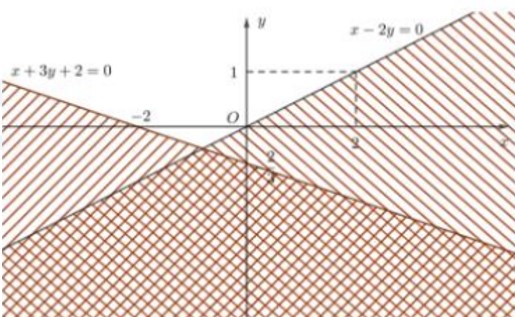
A. \(\left\{ \begin{array}{*{35}{l}} x-2y\ge 0 \\ x+3y\ge -2 \\ \end{array} \right.\)
B. \( \left\{ \begin{array}{*{35}{l}} x-2y\le 0 \\ x+3y\ge -2 \\ \end{array} \right.\)
C. \(\left\{ \begin{align} & x-2y<0 \\ & x+3y>-2 \\ \end{align} \right. \)
D. \(\left\{ \begin{array}{*{35}{l}} x-2y\le 0 \\ x+3y\le -2 \\ \end{array} \right.\)
CΟΔu 18: MαΜ΅nh ΡëαΜ¹ phαΜß ΡëαΜ΄nh cαΜßa mαΜ΅nh ΡëαΜ¹: " \(\exists x\in \mathbb{R},2{{x}^{2}}+3x-5<0\) " lΟ†
A. " \(\exists x\in \mathbb{R},2{{x}^{2}}+3x-5>0\) " B. " \(\forall x\in \mathbb{R},2{{x}^{2}}+3x-5>0\) "
C. " \(\exists x\in \mathbb{R},2{{x}^{2}}+3x-5\ge 0\) " D. "\(\forall x\in \mathbb{R},2{{x}^{2}}+3x-5\ge 0\) "
CΟΔu 19: Cho tam giΟΓc ABC, mαΜ΅nh ΡëαΜ¹ nΟ†o sau ΡëΟΔy ΡëΟΚng?
A. \({{a}^{2}}={{b}^{2}}+{{c}^{2}}+2bc\text{cos}A\). B. \({{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\text{cos}A\).
C. \({{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\text{cos}B\). D. \({{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\text{cos}C\).
CΟΔu 20: ΡêiαΜÉm \(O\left( 0;0 \right)\) khΟ¥ng thuαΜôc miαΜ¹n nghiαΜ¹m cαΜßa hαΜ΅ bαΚΞt phΤΑΤΓng trΟ§nh nΟ†o?
A. \(\left\{ \begin{array}{*{35}{l}} x+3y<0 \\ 2x+y+4>0 \\ \end{array} \right.\)
B. \(\left\{ \begin{array}{*{35}{l}} x+3y-6<0 \\ 2x+y+4\ge 0 \\ \end{array} \right.\)
C. \( \left\{ \begin{array}{*{35}{l}} x+3y-6<0 \\ 2x+y+4>0 \\ \end{array} \right.\)
D. \(\left\{ \begin{array}{*{35}{l}} x+3y\ge 0 \\ 2x+y-4<0 \\ \end{array} \right.\)
---(ΡêαΜÉ xem tiαΚΩp nΟ¥ΧΘi dung trΡÉΧ¹c nghiΟΣΧΘm cαΜßa ΡëαΜ¹ thi cΟΓc em vui lΟ≤ng xem tαΚΓi online hoαΚΖc ΡëΡÉng nhαΚ≠p vΟ†o HαΜ¨C247 ΡëαΜÉ tαΚΘi vαΜ¹ mΟΓy)---
B. TαΜΑ LUαΚ§N (3,0 ΡëiαΜÉm)
BΟ†i 1. Cho \(A=\left[ -5;2 \right);B=\left( 0;+\infty \right)\). TΟ§m \(A\cup B;A\cap B\) vΟ† biαΜÉu diαΜÖn kαΚΩt quαΚΘ trΟΣn trαΜΞc sαΜë.
BΟ†i 2. Trong lαΜ¦p 10A cΟ≥ 45 hαΜçc sinh trong ΡëΟ≥ cΟ≥ 25 em thΟ≠ch mΟ¥n VΡÉn, 20 em thΟ≠ch mΟ¥n ToΟΓn, 18 em thΟ≠ch mΟ¥n SαΜ≠, 6 em khΟ¥ng thΟ≠ch mΟ¥n nΟ†o, 5 em thΟ≠ch cαΚΘ ba mΟ¥n. HαΜèi sαΜë em thΟ≠ch chαΜâ mαΜôt mΟ¥n trong ba mΟ¥n trΟΣn.
BΟ†i 3. MαΜôt cΟ¥ng ty kinh doanh thΤΑΤΓng mαΚΓi chuαΚ©n bαΜ΄ cho mαΜôt ΡëαΜΘt khuyαΚΩn mαΚΓi nhαΚ±m thu hΟΚt khΟΓch hΟ†ng bαΚ±ng cΟΓch tiαΚΩn hΟ†nh quαΚΘng cΟΓo sαΚΘn phαΚ©m cαΜßa cΟ¥ng ty trΟΣn hαΚΩ thαΜëng phΟΓt thanh vΟ† truyαΜ¹n hΟ§nh. Chi phΟ≠ cho 1 phΟΚt quαΚΘng cΟΓo trΟΣn sΟ≥ng phΟΓt thanh lΟ† \(800000\) ΡëαΜ™ng, trΟΣn sΟ≥ng truyαΜ¹n hΟ§nh lΟ† \(4.000.000\). ΡêΟ†i phΟΓt thanh chαΜâ nhαΚ≠n phΟΓt cΟΓc chΤΑΤΓng trΟ§nh quαΚΘng cΟΓo dΟ†i Ο≠t nhαΚΞt lΟ† 5 phΟΚt. Do nhu cαΚßu quαΚΘng cΟΓo trΟΣn truyαΜ¹n hΟ§nh lαΜ¦n nΟΣn ΡëΟ†i truyαΜ¹n hΟ§nh chαΜâ nhαΚ≠n phΟΓt cΟΓc chΤΑΤΓng trΟ§nh dΟ†i tαΜëi Ρëa lΟ† 4 phΟΚt. Theo cΟΓc phΟΔn tΟ≠ch cΟΙng thαΜùi lΤΑαΜΘng mαΜôt phΟΚt quαΚΘng cΟΓo trΟΣn truyαΜ¹n hΟ§nh sαΚΫ cΟ≥ hiαΜ΅u quαΚΘ gαΚΞp 6 lαΚßn trΟΣn sΟ≥ng phΟΓt thanh. CΟ¥ng ty dαΜ± ΡëαΜ΄nh chi tαΜëi Ρëa lΟ† 16.000.000 ΡëαΜ™ng cho quαΚΘng cΟΓo. CΟ¥ng ty cαΚßn ΡëαΚΖt thαΜùi lΤΑαΜΘng quαΚΘng cΟΓo trΟΣn sΟ≥ng phΟΓt thanh vΟ† truyαΜ¹n hΟ§nh nhΤΑ thαΚΩ nΟ†o ΡëαΜÉ hiαΜ΅u quαΚΘ nhαΚΞt?
BΟ†i 4. TαΜΪ mαΜôt ΡëαΜânh thΟΓp chiαΜ¹u cao \(CD=80\text{ }\!\!~\!\!\text{ m}\), ngΤΑαΜùi ta nhΟ§n thαΚΞy hai ΡëiαΜÉm A vΟ† B trΟΣn mαΚΖt ΡëαΚΞt dΤΑαΜ¦i cΟΓc gΟ≥c nhΟ§n \({{60}^{\circ }}\) vΟ† \({{45}^{\circ }}\) (nhΤΑ hΟ§nh).
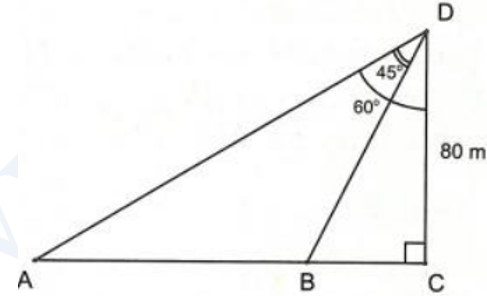
BiαΚΩt ba ΡëiαΜÉm A,B,C thαΚ≥ng hΟ†ng. TΟ≠nh khoαΚΘng cΟΓch \(AB\).
2. ΡêaΧ¹p aΧ¹n
A. TRαΚ°C NGHIαΜÜM (7,0 ΡëiαΜÉm)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
D |
B |
C |
B |
B |
C |
C |
B |
D |
A |
B |
C |
A |
A |
A |
C |
B |
|
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
D |
B |
A |
D |
D |
D |
B |
C |
A |
D |
C |
A |
D |
B |
B |
B |
D |
A |
B. TαΜΑ LUαΚ§N (3,0 ΡëiΟΣΧâm)
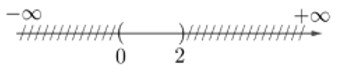
BΟ†i 1. Cho \(A=\left[ -5;2 \right);B=\left( 0;+\infty \right)\). TΟ§m A\cup B;A\cap B vΟ† biαΜÉu diαΜÖn kαΚΩt quαΚΘ trΟΣn trαΜΞc sαΜë.
LαΜùi giαΚΘi
\(A\cup B=\left[ -5;+\infty \right)\)

\(A\cap B=\left( 0;2 \right)\)
BΟ†i 2. Trong lαΜ¦p 10A cΟ≥ 45 hαΜçc sinh trong ΡëΟ≥ cΟ≥ 25 em thΟ≠ch mΟ¥n VΡÉn, 20 em thΟ≠ch mΟ¥n ToΟΓn, 18 em thΟ≠ch mΟ¥n SαΜ≠, 6 em khΟ¥ng thΟ≠ch mΟ¥n nΟ†o, 5 em thΟ≠ch cαΚΘ ba mΟ¥n. HαΜèi sαΜë em thΟ≠ch chαΜâ mαΜôt mΟ¥n trong ba mΟ¥n trΟΣn.
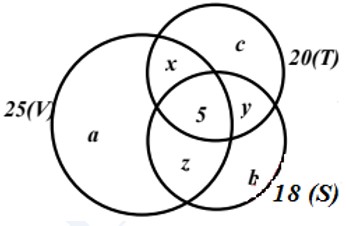
GαΜçi a,b,c theo thαΜ© tαΜ± lΟ† sαΜë hαΜçc sinh chαΜâ thΟ≠ch mΟ¥n vΡÉn, sαΜ≠, toΟΓn.
x lΟ† sαΜë hαΜçc sinh chαΜâ thΟ≠ch hai mΟ¥n vΡÉn vΟ† toΟΓn.
y lΟ† sαΜë hαΜçc sinh chαΜâ thΟ≠ch hai mΟ¥n sαΜ≠ yΟΔ toΟΓn.
z lΟ† sαΜë hαΜçc sinh chαΜâ thΟ≠ch hai mΟ¥n vΡÉn vΟ† sαΜ≠
DαΜ±a vΟ†o biαΜÉu ΡëαΜ™ ven ta cΟ≥ hαΜ΅ phΤΑΤΓng trΟ§nh:
\(\left\{ \begin{array}{*{35}{l}} a+x+z+5=25 \\ b+y+z+5=18 \\ c+x+y+5=20 \\ x+y+z+a+b+c+5=39 \\ \end{array} \right.\)
GiαΚΘi hαΜ΅ phΤΑΤΓng trΟ§nh ta ΡëΤΑαΜΘc \(a+b+c=20\).
VαΚ≠y sαΜë em thΟ≠ch chi mαΜôt mΟ¥n trong ba mΟ¥n trΟΣn lΟ† 20.
---(ΡêαΜÉ xem tiαΚΩp ΡëaΧ¹p aΧ¹n cαΜßa ΡëαΜ¹ thi cΟΓc em vui lΟ≤ng xem tαΚΓi online hoαΚΖc ΡëΡÉng nhαΚ≠p vΟ†o HαΜ¨C247 ΡëαΜÉ tαΚΘi vαΜ¹ mΟΓy)---
TrΟΣn ΡëΟΔy lΟ† mΟ¥ΧΘt phΟΔΧÄn nαΜôi dung tΟ†i liαΜ΅u ΡêΟΣΧÄ thi giΤΑΧÉa HK1 mΟ¥n ToaΧ¹n 10 CTST nΡÉm hoΧΘc 2023 - 2024 TrΤΑΤΓΧÄng THPT TΤΑΧ¹ KiΟΣΧΘt coΧ¹ ΡëaΧ¹p aΧ¹n. ΡêαΜÉ xem thΟΣm nhiαΜ¹u tΟ†i liαΜ΅u tham khαΚΘo hαΜ·u Ο≠ch khΟΓc cΟΓc em chαΜçn chαΜ©c nΡÉng xem online hoαΚΖc ΡëΡÉng nhαΚ≠p vΟ†o trang hoc247.net ΡëαΜÉ tαΚΘi tΟ†i liαΜ΅u vαΜ¹ mΟΓy tΟ≠nh.
Hy vαΜçng tΟ†i liαΜ΅u nΟ†y sαΚΫ giΟΚp cΟΓc em hαΜçc sinh Ο¥n tαΚ≠p tαΜët vΟ† ΡëαΚΓt thΟ†nh tΟ≠ch cao trong kΟ§ thi sαΚ·p tαΜ¦i!
TΤΑ liαΜ΅u nαΜïi bαΚ≠t tuαΚßn
- Xem thΟΣm
ERROR:connection to 10.20.1.101:9312 failed (errno=111, msg=Connection refused)
ERROR:connection to 10.20.1.101:9312 failed (errno=111, msg=Connection refused)


