Phᚧn hÆ°áŧng dášŦn giášĢi bà i tášp ToÃĄn 8 CÃĄnh Diáŧu ChÆ°ÆĄng 7 Bà i 1 PhÆ°ÆĄng trÃŽnh bášc nhášĨt máŧt ášĐn sáš― giÚp cÃĄc em nášŊm ÄÆ°áŧĢc phÆ°ÆĄng phÃĄp và rÃĻn luyáŧn kÄĐ nÄng, giášĢi bà i tášp táŧŦ SGK ToÃĄn 8 Tášp 2 CÃĄnh Diáŧu.
-
HoaĖĢt ÄÃīĖĢng 1 trang 39 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Trong bà i toÃĄn nÊu áŧ phᚧn máŧ Äᚧu, hÃĢy viášŋt:
a) CÃĄc biáŧu tháŧĐc \(A\left( x \right),\,\,B\left( x \right)\) lᚧn lÆ°áŧĢt biáŧu tháŧ (theo \(x\)) táŧng kháŧi lÆ°áŧĢng cÃĄc háŧp xášŋp áŧ ÄÄĐa cÃĒn bÊn trÃĄi, ÄÄĐa cÃĒn bÊn phášĢi;
b) Háŧ tháŧĐc tháŧ hiáŧn sáŧą bášąng nhau cáŧ§a hai biáŧu tháŧĐc trÊn.
-
HoaĖĢt ÄÃīĖĢng 2 trang 40 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Khi \(x = 4\), tÃnh giÃĄ tráŧ máŧi vášŋ cáŧ§a phÆ°ÆĄng trÃŽnh: \(3x + 4 = x + 12\,\,\left( 1 \right)\). So sÃĄnh hai giÃĄ tráŧ ÄÃģ?
-
HoaĖĢt ÄÃīĖĢng 3 trang 40 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Quan sÃĄt phÆ°ÆĄng trÃŽnh (ášĐn \(x\)): \(4x + 12 = 0\), nÊu nhášn xÃĐt váŧ bášc cáŧ§a Äa tháŧĐc áŧ vášŋ trÃĄi cáŧ§a phÆ°ÆĄng trÃŽnh ÄÃģ?
-
Luyáŧn tášp 1 trang 40 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
NÊu hai và dáŧĨ váŧ phÆ°ÆĄng trÃŽnh bášc nhášĨt ášĐn \(x\)?
- VIDEOYOMEDIA
-
Luyáŧn tášp 2 trang 40 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Kiáŧm tra xem \(x = - 3\) cÃģ là nghiáŧm cáŧ§a phÆ°ÆĄng trÃŽnh bášc nhášĨt \(5x + 15 = 0\) hay khÃīng?
-
HoaĖĢt ÄÃīĖĢng 4 trang 41 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
NÊu quy tášŊc chuyáŧn vášŋ trong máŧt Äášģng tháŧĐc sáŧ?
-
HoaĖĢt ÄÃīĖĢng 5 trang 41 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
XÃĐt Äášģng tháŧĐc sáŧ: \(2 + 3 - 4 = 9 - 10 + 2\). TÃnh giÃĄ tráŧ máŧi vášŋ cáŧ§a Äášģng tháŧĐc ÄÃģ khi nhÃĒn cášĢ hai vášŋ váŧi 5 và so sÃĄnh hai giÃĄ tráŧ nhášn ÄÆ°áŧĢc?
-
Luyáŧn tášp 3 trang 42 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
GiášĢi cÃĄc phÆ°ÆĄng trÃŽnh:
a) \( - 6x - 15 = 0\);
b) \( - \frac{9}{2}x + 21 = 0.\)
-
Luyáŧn tášp 4 trang 42 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
GiášĢi phÆ°ÆĄng trÃŽnh: \(2\left( {x - 0,7} \right) - 1,6 = 1,5 - \left( {x + 1,2} \right)\).
-
BaĖi 1 trang 43 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Kiáŧm tra xem sáŧ nà o là nghiáŧm cáŧ§a phÆ°ÆĄng trÃŽnh tÆ°ÆĄng áŧĐng sau ÄÃĒy.
a) \(3x + 9 = 0\) váŧi \(x = 3;\,\,x = - 3\).
b) \(2 - 2x = 3x + 1\) váŧi \(x = - \frac{1}{5};\,\,x = \frac{1}{5}\).
-
BaĖi 2 trang 43 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
TÃŽm cháŧ sai trong máŧi láŧi giášĢi sau và giášĢi lᚥi cho ÄÚng:
a)
\(\begin{array}{*{35}{l}} 5-\left( x+8 \right)=3x+3\left( x-9 \right) \\ \Leftrightarrow 5-x+8=3x+3x-27 \\ \Leftrightarrow 13-x=6x-27 \\ \Leftrightarrow -x-6x=-27+13 \\ \Leftrightarrow -7x=-14 \\ \Leftrightarrow x=\left( -14 \right):\left( -7 \right) \\ \Leftrightarrow x=2 \\ \end{array}\)
Vášy phÆ°ÆĄng trÃŽnh cÃģ nghiáŧm \(x = 2\).
b)
\(\begin{array}{*{35}{l}} 3x-18+x=12-\left( 5x+3 \right) \\ \Leftrightarrow 4x-18=12-5x-3 \\ \Leftrightarrow 4x+5x=9-18 \\ \Leftrightarrow 9x=-9 \\ \Leftrightarrow x=\left( -9 \right):9 \\ \Leftrightarrow x=-1 \\ \end{array}\)
Vášy phÆ°ÆĄng trÃŽnh cÃģ nghiáŧm \(x = - 1\).
-
BaĖi 3 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
GiášĢi cÃĄc phÆ°ÆĄng trÃŽnh sau:
a) \(6x + 4 = 0\);
b) \( - 14x - 28 = 0\);
c) \(\frac{1}{3}x - 5 = 0\);
d) \(3y - 1 = - y + 19\);
e) \( - 2\left( {z + 3} \right) - 5 = z + 4\);
g) \(3\left( {t - 10} \right) = 7\left( {t - 10} \right)\)
-
BaĖi 4 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
GiášĢi cÃĄc phÆ°ÆĄng trÃŽnh:
a) \(\frac{{5x - 2}}{3} = \frac{{5 - 3x}}{2}\);
b) \(\frac{{10x + 3}}{{12}} = 1 + \frac{{6 + 8x}}{9}\);
c) \(\frac{{7x - 1}}{6} + 2x = \frac{{16 - x}}{5}\).
-
BaĖi 5 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
TÃŽm \(x\), biášŋt táŧĐ giÃĄc \(ABCD\) là hÃŽnh vuÃīng (HÃŽnh 2)?
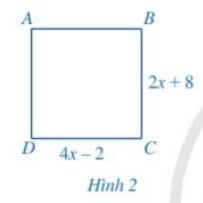
-
BaĖi 6 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
HÃŽnh tam giÃĄc và hÃŽnh cháŧŊ nhášt áŧ HÃŽnh 3 cÃģ cÃđng chu vi. Viášŋt phÆ°ÆĄng trÃŽnh biáŧu tháŧ sáŧą bášąng nhau cáŧ§a chu vi hÃŽnh tam giÃĄc, hÃŽnh cháŧŊ nhášt ÄÃģ và tÃŽm \(x\)?

-
BaĖi 7 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
Trong phÃēng thà nghiáŧm, cháŧ Loan sáŧ dáŧĨng cÃĒn Roberval Äáŧ cÃĒn: bÊn ÄÄĐa tháŧĐ nhášĨt Äáš·t máŧt quášĢ cÃĒn náš·ng 500 g; bÊn ÄÄĐa tháŧĐ hai Äáš·t hai vášt cÃđng cÃĒn náš·ng \(x\) g và ba quášĢ cÃĒn nháŧ, máŧi quášĢ cÃĒn ÄÃģ náš·ng 50 g. Cháŧ Loan thášĨy cÃĒn thÄng bášąng. Viášŋt phÆ°ÆĄng trÃŽnh biáŧu tháŧ sáŧą thÄng bášąng cáŧ§a cÃĒn khi ÄÃģ?
-
BaĖi 8 trang 44 SGK ToaĖn 8 TÃĒĖĢp 2 CaĖnh diÊĖu - CD
HÃŽnh 4 mÃī tášĢ máŧt Äà i phun nÆ°áŧc. Táŧc Äáŧ ban Äᚧu cáŧ§a nÆ°áŧc là 48 ft/s (ft là máŧt ÄÆĄn váŧ Äo Äáŧ dà i váŧi 1 ft = 0,3048 m). Táŧc Äáŧ \(v\) (ft/s) cáŧ§a nÆ°áŧc tᚥi tháŧi Äiáŧm \(t\) (s) ÄÆ°áŧĢc cho báŧi cÃīng tháŧĐc \(v = 48 - 32t\). TÃŽm tháŧi gian Äáŧ máŧt giáŧt nÆ°áŧc Äi táŧŦ máš·t Äà i phun nÆ°áŧc Äášŋn khi Äᚥt Äáŧ cao táŧi Äa?