Giải bài 4.2 tr 28 sách BT Toán lớp 8 Tập 1
Cho hai phân thức \(\displaystyle {1 \over {{x^2} + ax - 2}}\), \(\displaystyle{2 \over {{x^2} + 5x + b}}\). Hãy xác định \(a\) và \(b\) biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là \({x^3} + 4{x^2} + x - 6\). Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là \({x^3} + 4{x^2} + x - 6\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
* Phép chia hết là phép chia có số dư bằng \(0\).
* Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.
- Tìm nhân tử phụ của mỗi mẫu thức.
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Lời giải chi tiết
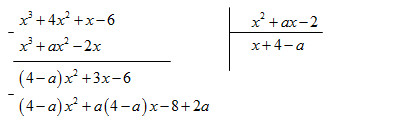
Vì phép chia này là phép chia hết nên số dư phải bằng 0
\( \Rightarrow a\left( {4 - a} \right) = 3\) (1) và \(2a - 8 = - 6\) (2)
Từ (2) \( \Rightarrow 2a - 8 = - 6 \Rightarrow a = 1\)
a = 1 thỏa mãn (1) ta có phân thức \({1 \over {{x^2} + x - 2}}\)
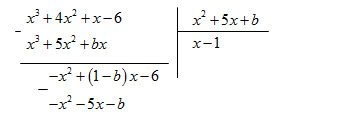
Vì phép chia này là phép chia hết nên số dư phải bằng 0
\( \Rightarrow \left( {1 - b} \right) = 5\) (3) và – b = − 6 (4)
Từ (4) ⇒ − b = − 6 ⇒ b = 6
b = 6 thỏa mãn (3) ta có phân thức \({2 \over {{x^2} + 5x + 6}}\)
\(\eqalign{ & {1 \over {{x^2} + x - 2}} = {{\left( {x + 3} \right)} \over {\left( {{x^2} + x - 2} \right)\left( {x + 3} \right)}} = {{x + 3} \over {{x^3} + 4{x^2} + x - 6}} \cr & {2 \over {{x^2} + 5x + 6}} = {{2\left( {x - 1} \right)} \over {\left( {{x^2} + 5x + 6} \right)\left( {x - 1} \right)}} = {{2x - 2} \over {{x^3} + 4{x^2} + x - 6}} \cr} \)
-- Mod Toán 8 HỌC247
-


Bài 13 trang 27 sách bài tập toán 8 tập 1
bởi Nguyễn Trà Giang
 15/10/2018
15/10/2018
Bài 13 (Sách bài tập - trang 27)
Quy đồng mẫu thức các phân thức sau :
a) \(\dfrac{25}{14x^2y};\dfrac{14}{21xy^5}\)
b) \(\dfrac{11}{102x^4y};\dfrac{3}{34xy^3}\)
c) \(\dfrac{3x+1}{12xy^4};\dfrac{y-2}{9x^2y^3}\)
d) \(\dfrac{1}{6x^3y^2};\dfrac{x+1}{9x^2y^4};\dfrac{x-1}{4xy^3}\)
e) \(\dfrac{3+2x}{10x^4y};\dfrac{5}{8x^2y^2};\dfrac{2}{3xy^5}\)
f) \(\dfrac{4x-4}{2x\left(x+3\right)};\dfrac{x-3}{3x\left(x+1\right)}\)
g) \(\dfrac{2x}{\left(x+2\right)^3};\dfrac{x-2}{2x\left(x+2\right)^2}\)
h) \(\dfrac{5}{3x^3-12x};\dfrac{3}{\left(2x+4\right)\left(x+3\right)}\)
Theo dõi (0) 1 Trả lời -


rút gọn
bởi Lê Thánh Tông
 25/07/2018
25/07/2018
các bạn cho mình hỏi bài này với
Rút gọn biểu thức
\(B = \left( {ab + bc + ca} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) - abc\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)\)
Theo dõi (0) 2 Trả lời -


Các bạn ơi cho mình hỏi, quy đồng là làm cho mẫu nó giống nhau đúng hok vậy?
Theo dõi (0) 1 Trả lời -


Quy đồng mẫu thức
bởi Thùy Nguyễn
 14/09/2017
14/09/2017
Các bạn ơi giúp mình bài này với, mình tính ra A mà sao đáp án ra C
Kết quả của phép tính sau là?
\(\frac{2}{{x + 3}} + \frac{3}{{{x^2} - 9}}\)
A.\(\frac{{2x + 9}}{{{x^2} - 9}}\)
B.\(\frac{5}{{{x^2} - 9}}\)
C.\(\frac{{2x - 3}}{{{x^2} - 9}}\)
Theo dõi (0) 2 Trả lời -
ADMICRO


Quy đồng mẫu thức
bởi Phong Vu
 08/09/2017
08/09/2017
Bài này mình giải vầy đúng k các bạn, mình giải xong thấy sao sao ak, nhưng xem đi xem lại không thấy sai gì.Bạn nào tốt bụng kiểm tra giúp mình với
\(\begin{array}{l} \,\,\,\,\,\,\frac{x}{{x + 1}} + \frac{2}{{{x^2} - 1}} + \frac{3}{{x - 1}}\\ = \frac{{x(x - 1) + 2(x + 1) - 3(x + 1)}}{{(x + 1)(x - 1)}}\\ = \frac{{{x^2} - x + 2x + 2 - 3x - 3}}{{(x + 1)(x - 1)}}\\ = \frac{{{x^2} - 2x - 1}}{{(x + 1)(x - 1)}} \end{array}\)
Theo dõi (0) 2 Trả lời -


Quy đồng
bởi Thùy Trang
 08/09/2017
08/09/2017
Giúp mình bài quy đồng này với nha các bợn ^^! Mình cảm ơn
\(\frac{{3x}}{{2x + 4}}\) và \(\frac{{x + 3}}{{{x^2} - 4}}\)
Ta có:
2x+4=2(x+2)
x2-4=(x-2)(x+2)
=> Mẫu chung là : 2(x+2)(x-2)
\(\frac{{3x}}{{2x + 4}} = \frac{{3x(x - 2)}}{{2(x + 2)(x - 2)}} = \frac{{3{x^2} - 6x}}{{2(x + 2)(x - 2)}}\)
\(\frac{{x + 3}}{{{x^2} - 4}} = \frac{{(x + 3).2}}{{(x + 2)(x - 2).2}} = \frac{{2x + 6}}{{2(x + 2)(x - 2)}}\)
Theo dõi (0) 1 Trả lời


