Trong bΟ†i hαΜçc HΟ†m sαΜë bαΚ≠c nhαΚΞt y = ax + b (a β↠0) cαΜßa chΤΑΤΓng trΟ§nh mΟ¥n ToΟΓn 8 CΟΓnh DiαΜ¹u, cΟΓc em sαΚΫ biαΚΩt cΟΓch lαΚ≠p bαΚΘng giΟΓ trαΜ΄, vαΚΫ ΡëαΜ™ thαΜ΄ cαΜßa ΡëαΜ™ thαΜ΄ hΟ†m sαΜë. CΟΓc kiαΚΩn thαΜ©c nΟ†y sαΚΫ giΟΚp cΟΓc em ΟΓp dαΜΞng ΡëαΜÉ giαΚΘi quyαΚΩt cΟΓc bΟ†i toΟΓn thαΜ±c tαΚΩ. ChΟΚc cΟΓc em hαΜçc thαΚ≠t tαΜët!
TΟ≥m tαΚ·t lΟΫ thuyαΚΩt
1.1. ΡêαΜ΄nh nghΡ©a
| HΟ†m sαΜë bαΚ≠c nhαΚΞt lΟ† hΟ†m sαΜë ΡëΤΑαΜΘc cho bαΜüi cΟ¥ng thαΜ©c y = ax +b, trong ΡëΟ≥ a, b lΟ† cΟΓc sαΜë cho trΤΑαΜ¦c vΟ† a khΟΓc 0. |
ChΟΚ ΟΫ: Khi b = 0, ta cΟ≥ hΟ†m sαΜë y = ax.
VΟ≠ dαΜΞ:
- HΟ†m sαΜë y = 2x + 3 lΟ† hΟ†m sαΜë bαΚ≠c nhαΚΞt vαΜ¦i hαΜ΅ sαΜë a = 2; b = 3.
- HΟ†m sαΜë y = 4x lΟ† hΟ†m sαΜë bαΚ≠c nhαΚΞt vαΜ¦i hαΜ΅ sαΜë a = 4; b = 0.
- HΟ†m sαΜë y = 0x βÄ™ 1 khΟ¥ng lΟ† hΟ†m sαΜë bαΚ≠c nhαΚΞt vΟ§ a = 0.
1.2. αΜ®ng dαΜΞng
VΟ≠ dαΜΞ: GiΟΓ bΟΓn 1 kg vαΚΘi thiαΜ¹u loαΚΓi I lΟ† 35 000 ΡëαΜ™ng.
a) ViαΚΩt cΟ¥ng thαΜ©c biαΜÉu thαΜ΄ sαΜë tiαΜ¹n y (ΡëαΜ™ng) thu ΡëΤΑαΜΘc khi bΟΓn x kg vαΚΘi thiαΜ¹u loαΚΓi I. HαΜèi y cΟ≥ phαΚΘi lΟ† hΟ†m sαΜë bαΚ≠c nhαΚΞt cαΜßa x hay khΟ¥ng?
b) TΟ≠nh sαΜë tiαΜ¹n thu ΡëΤΑαΜΘc khi bΟΓn 15 kg vαΚΘi thiαΜ¹u loαΚΓi I?
c) CαΚßn bΟΓn bao nhiΟΣu kg vαΚΘi thiαΜ¹u loαΚΓi I ΡëαΜÉ thu ΡëΤΑαΜΘc sαΜë tiαΜ¹n 1 400 000 ΡëαΜ™ng?
HΤΑαΜ¦ng dαΚΪn giαΚΘi
a) CT biαΜÉu thαΜ΄ sαΜë tiαΜ¹n y (ΡëαΜ™ng) thu ΡëΤΑαΜΘc khi bΟΓn x kg vαΚΘi thiαΜ¹u loαΚΓi I lΟ†:
y = 35 000x
Do ΡëΟ≥ y lΟ† hΟ†m sαΜë bαΚ≠c nhαΚΞt cαΜßa x.
b) SαΜë tiαΜ¹n thu ΡëΤΑαΜΘc khi bΟΓn 15 kg vαΚΘi thiαΜ¹u loαΚΓi I lΟ†:
35 000.15 = 525 000 (ΡëαΜ™ng)
VαΚ≠y sαΜë tiαΜ¹n thu ΡëΤΑαΜΘc khi bΟΓn 15 kg vαΚΘi thiαΜ¹u loαΚΓi I lΟ† 525 000 ΡëαΜ™ng.
c) SαΜë kg vαΚΘi thiαΜ¹u loαΚΓi I ΡëαΜÉ thu ΡëΤΑαΜΘc sαΜë tiαΜ¹n 1 400 000 ΡëαΜ™ng lΟ†:
1 400 000 : 35 000 = 40 (kg)
VαΚ≠y cαΚßn bΟΓn 40 kg vαΚΘi thiαΜ¹u loαΚΓi I ΡëαΜÉ thu ΡëΤΑαΜΘc sαΜë tiαΜ¹n 1 400 000 ΡëαΜ™ng.
BΟ†i tαΚ≠p minh hαΜça
BΟ†i 1: XΟΓc ΡëαΜ΄nh cΟΓc hαΜ΅ sαΜë cαΜßa x, hαΜ΅ sαΜë tαΜ± do trong mαΜ½i hΟ†m sαΜë bαΚ≠c nhαΚΞt sau:
a) y = 3x βÄ™ 4
b) y = β࣠x + 2
c)
HΤΑαΜ¦ng dαΚΪn giαΚΘi
a) HαΜ΅ sαΜë cαΜßa x lΟ† 3; hαΜ΅ sαΜë tαΜ± do lΟ† β࣠4.
b) HαΜ΅ sαΜë cαΜßa x lΟ† β࣠1; hαΜ΅ sαΜë tαΜ± do lΟ† 2.
c) HαΜ΅ sαΜë cαΜßa x lΟ† ; hαΜ΅ sαΜë tαΜ± do lΟ† 0.
BΟ†i 2: Cho hΟ†m sαΜë bαΚ≠c nhαΚΞt f(x) = x βà£1. TΟ≠nh f (1); f(0); f(βà£2).
HΤΑαΜ¦ng dαΚΪn giαΚΘi
Ta cΟ≥: f(1) = 1 βà£1 = 0; f(0) = 0 βà£1 = βà£1; f(βà£2) = βà£2 βà£1 = βà£3.
VαΚ≠y f(1) = 0; f(0) = βà£1; f(βà£2) = βà£3.
BΟ†i 3: GiΟΓ cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi cαΜë ΡëαΜ΄nh cαΜßa mαΜôt hΟΘng viαΜÖn thΟ¥ng bao gαΜ™m cΤΑαΜ¦c thuΟΣ bao lΟ† 22000 ΡëαΜ™ng/thΟΓng vΟ† cΤΑαΜ¦c gαΜçi lΟ† 800 ΡëαΜ™ng/phΟΚt.
a) LαΚ≠p cΟ¥ng thαΜ©c tΟ≠nh sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi y (ΡëαΜ™ng) phαΚΘi trαΚΘ trong thΟΓng khi gαΜçi x phΟΚt?
b) TΟ≠nh sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ khi gαΜçi 75 phΟΚt?
c) NαΚΩu sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ lΟ† 94 000 ΡëαΜ™ng thΟ§ trong thΟΓng ΡëΟ≥ thuΟΣ bao ΡëΟΘ gαΜçi bao nhiΟΣu phΟΚt?
HΤΑαΜ¦ng dαΚΪn giαΚΘi
a) CΟ¥ng thαΜ©c tΟ≠nh sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi y (ΡëαΜ™ng) phαΚΘi trαΚΘ trong thΟΓng khi gαΜçi x phΟΚt lΟ†:
y = 800x + 22 000
b) SαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ khi gαΜçi 75 phΟΚt lΟ†:
y = 800.75 + 22 000 = 82 000 (ΡëαΜ™ng)
VαΚ≠y sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ khi gαΜçi 75 phΟΚt lΟ† 82 000 ΡëαΜ™ng.
c) SαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ lΟ† 94000 ΡëαΜ™ng thΟ§ trong thΟΓng ΡëΟ≥ thuΟΣ bao ΡëΟΘ gαΜçi sαΜë phΟΚt lΟ†:
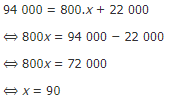
VαΚ≠y nαΚΩu sαΜë tiαΜ¹n cΤΑαΜ¦c ΡëiαΜ΅n thoαΚΓi phαΚΘi trαΚΘ lΟ† 94 000 ΡëαΜ™ng thΟ§ trong thΟΓng ΡëΟ≥ thuΟΣ bao ΡëΟΘ gαΜçi 90 phΟΚt.
3. LuyαΜ΅n tαΚ≠p BΟ†i 3 ChΤΑΤΓng 3 ToΟΓn 8 CΟΓnh DiαΜ¹u
Qua bΟ†i hαΜçc nΟ†y, cΟΓc em sαΚΫ hoΟ†n thΟ†nh mαΜôt sαΜë mαΜΞc tiΟΣu mΟ† bΟ†i ΡëΤΑa ra nhΤΑ sau:
- NhαΚ≠n biαΚΩt ΡëΤΑαΜΘc hΟ†m sαΜë bαΚ≠c nhαΚΞt.
- VαΚ≠n dαΜΞng hΟ†m sαΜë bαΚ≠c nhαΚΞt vΟ†o giαΚΘi quyαΚΩt mαΜôt sαΜë bΟ†i toΟΓn thαΜ±c tiαΜÖn.
3.1. TrαΚ·c nghiαΜ΅m BΟ†i 3 ChΤΑΤΓng 3 ToΟΓn 8 CΟΓnh DiαΜ¹u
CΟΓc em cΟ≥ thαΜÉ hαΜ΅ thαΜëng lαΚΓi nαΜôi dung kiαΚΩn thαΜ©c ΡëΟΘ hαΜçc ΡëΤΑαΜΘc thΟ¥ng qua bΟ†i kiαΜÉm tra TrαΚ·c nghiαΜ΅m ToΟΓn 8 CΟΓnh DiαΜ¹u ChΤΑΤΓng 3 BΟ†i 3 cαΜ±c hay cΟ≥ ΡëΟΓp ΟΓn vΟ† lαΜùi giαΚΘi chi tiαΚΩt.
CΟΔu 4-10: MαΜùi cΟΓc em ΡëΡÉng nhαΚ≠p xem tiαΚΩp nαΜôi dung vΟ† thi thαΜ≠ Online ΡëαΜÉ cαΜßng cαΜë kiαΚΩn thαΜ©c vΟ† nαΚ·m vαΜ·ng hΤΓn vαΜ¹ bΟ†i hαΜçc nΟ†y nhΟ©!
3.2. BΟ†i tαΚ≠p SGK BΟ†i 3 ChΤΑΤΓng 3 ToΟΓn 8 CΟΓnh DiαΜ¹u
CΟΓc em cΟ≥ thαΜÉ xem thΟΣm phαΚßn hΤΑαΜ¦ng dαΚΪn GiαΚΘi bΟ†i tαΚ≠p ToΟΓn 8 CΟΓnh DiαΜ¹u ChΤΑΤΓng 3 BΟ†i 3 ΡëαΜÉ giΟΚp cΟΓc em nαΚ·m vαΜ·ng bΟ†i hαΜçc vΟ† cΟΓc phΤΑΤΓng phΟΓp giαΚΘi bΟ†i tαΚ≠p.
KhαΜüi ΡëαΜông trang 67 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
HoαΚΓt ΡëαΜông 1 trang 67 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
LuyαΜ΅n tαΚ≠p 1 trang 67 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
LuyαΜ΅n tαΚ≠p 2 trang 68 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
LuyαΜ΅n tαΚ≠p 3 trang 69 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BΟ†i 1 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BaΧÄi 2 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BaΧÄi 3 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BaΧÄi 3 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BaΧÄi 5 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
BΟ†i 6 trang 70 SGK ToaΧ¹n 8 TΟΔΧΘp 1 CaΧ¹nh diΟΣΧÄu - CD
4. HαΜèi ΡëΟΓp BΟ†i 3 ChΤΑΤΓng 3 ToΟΓn 8 CΟΓnh DiαΜ¹u
Trong quΟΓ trΟ§nh hαΜçc tαΚ≠p nαΚΩu cΟ≥ thαΚ·c mαΚ·c hay cαΚßn trαΜΘ giΟΚp gΟ§ thΟ§ cΟΓc em hΟΘy comment αΜü mαΜΞc HαΜèi ΡëΟΓp, CαΜông ΡëαΜ™ng ToΟΓn HOC247 sαΚΫ hαΜ½ trαΜΘ cho cΟΓc em mαΜôt cΟΓch nhanh chΟ≥ng!
ChΟΚc cΟΓc em hαΜçc tαΚ≠p tαΜët vΟ† luΟ¥n ΡëαΚΓt thΟ†nh tΟ≠ch cao trong hαΜçc tαΚ≠p!
-- Mod ToΟΓn HαΜçc 8 HαΜ¨C247








