Giải bài 9.14 trang 55 SBT Toán 7 Kết nối tri thức tập 2
Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho \(AM = \dfrac{3}{2}AG;AN = 2AM\). Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B.
a)Chứng minh hai tam giác ABM và NCM bằng nhau, từ đó suy ra AM là đường trung tuyến của tam giác ABC.
b) Chứng minh rằng G là trọng tâm của tam giác ABC vừa dựng được.
Hướng dẫn giải chi tiết
Phương pháp giải:
a)Chứng minh: \(\Delta ABM = \Delta NCM\left( {g - c - g} \right)\)
b)Chứng minh: \(AG = \dfrac{2}{3}AM\).
Lời giải chi tiết:
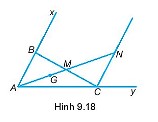
a)
Xét \(\Delta ABM\)và \(\Delta NCM\) có:
\(\widehat {MAB} = \widehat {MNC}\)(2 góc so le trong NC // Ax)
\(\widehat {AMB} = \widehat {NMC}\)(2 góc đối đỉnh)
AN = 2AM =>AM = NM
\( \Rightarrow \Delta ABM = \Delta NCM\left( {g - c - g} \right)\)
\( \Rightarrow MB = MC\)(cạnh tương ứng)
\( \Rightarrow M\)là trung điểm của BC
Vậy AM là đường trung tuyến của tam giác ABC.
b)
Ta có: Điểm G nằm trên đường trung tuyến AM của tam giác ABC
\(AM = \dfrac{3}{2}AG \Rightarrow AG = \dfrac{2}{3}AM\)
Vậy G là trọng tâm tam giác ABC.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 9.24 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.25 trang 76 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.15 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.15 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.16 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.17 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.18 trang 55 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


