Giải bài 6 trang 27 SGK Toán 7 Chân trời sáng tạo tập 1
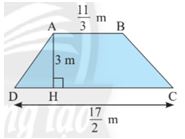
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
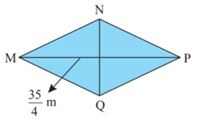
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP= \(\frac{{35}}{4}\)m. Tính độ dài NQ.
Hướng dẫn giải chi tiết Giải bài 6 trang 27
Phương pháp giải
a) Diện tích hình thang =(đáy lớn+đáy nhỏ).chiều cao:2
b) Diện tích hình thoi= tích hai đường chéo:2
Lời giải chi tiết
a) Diện tích hình thang là:
\(\left( {AB + DC} \right).AH:2 = \left( {\frac{{11}}{3} + \frac{{17}}{2}} \right).3:2 = \frac{{73}}{4}\)(cm2)
b) Ta có diện tích hình thoi MNPQ là \(\frac{{73}}{4}\,c{m^2}\)
Nên ta có:
\(\begin{array}{ccccc}{S_{MNPQ}} = \frac{{73}}{4} \Rightarrow MP.NQ:2 = \frac{{73}}{4}\\ \Rightarrow \frac{{35}}{4}.NQ:2 = \frac{{73}}{4}\\ \Rightarrow \frac{{35}}{8}.NQ= \frac{{73}}{4} \Rightarrow NQ = \frac{{73}}{4}:\frac{{35}}{8} = \frac{{146}}{{35}}\end{array}\)
Vậy \(NQ = \frac{{146}}{{35}}\)cm.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 4 trang 27 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 27 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 28 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 28 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 28 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 28 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 28 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 19 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 20 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 20 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 20 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 20 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
-

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính một cách hợp lí: \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\);
bởi Thu Hang
 26/11/2022
Theo dõi (0) 1 Trả lời
26/11/2022
Theo dõi (0) 1 Trả lời