Giải bài 59 trang 86 SBT Toán 7 Cánh diều tập 2
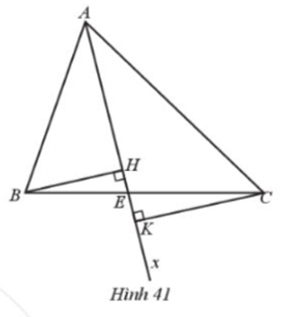
Cho tam giác ABC có \(\widehat B\) và \(\widehat C\) nhọn. H và K lần lượt là hình chiếu của B và C trên Ax (Hình 41).
Hướng dẫn giải chi tiết Bài 59
Phương pháp giải
- Sử dụng trong tam giác vuông, cạnh huyền là cạnh lớn nhất để chứng minh \(BH + CK \le BC\)
- Tìm điều kiện BH + CK lớn nhất khi nào?
Lời giải chi tiết
a) Vì ∆BHE vuông tại H nên BH ≤ BE (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).
Vì ∆CKE vuông tại K nên CK ≤ CE (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).
Suy ra BH + CK ≤ BE + CE = BC.
Vậy BH + CK ≤ BC.
b) Ta có BH + CK ≤ BC (theo câu a).
Do đó BH + CK lớn nhất khi BH + CK = BC
Điều này xảy ra khi và chỉ khi BH = BE, CK = CE.
Khi đó BH ≡ BE, CK ≡ CE
Do đó BE ⊥ Ax và CE ⊥ Ax
Hay BC ⊥ Ax.
Vậy nếu tổng BH + CK lớn nhất thì tia Ax phải vuông góc với BC.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


