Giải bài 3 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1
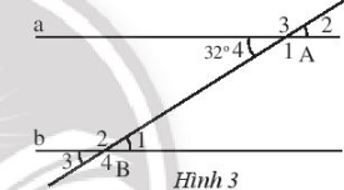
Trong Hình 3 cho biết a // b. Tìm số đo các góc đỉnh A và B.
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Ta sử dụng tính chất 2 góc so le trong để tính góc B1 sau đó dùng tính chất 2 góc kề bù và 2 góc đối đỉnh để tính lần lượt các góc đỉnh B
Lời giải chi tiết
– Tại đỉnh A:
• Vì \(\widehat {{A_2}}\)và \(\widehat {{A_4}}\) là hai góc đối đỉnh nên \(\widehat {{A_2}}\)=\(\widehat {{A_4}}\)=32°.
• Vì \(\widehat {{A_1}}\) và \(\widehat {{A_4}}\) là hai góc kề bù nên ta có:
\(\widehat {{A_1}}\)+\(\widehat {{A_4}}\)=180°
Suy ra \(\widehat {{A_1}}\)=180°−\(\widehat {{A_4}}\)=180°−32°=148°
• Vì \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\)=\(\widehat {{A_3}}\)=148°.
– Tại đỉnh B:
Vì a // b nên:
• \(\widehat {{B_1}}\)=\(\widehat {{A_4}}\)=32° (hai góc so le trong)
• \(\widehat {{B_2}}\)=\(\widehat {{A_1}}\)=148° (hai góc so le trong)
• \(\widehat {{B_3}}\)=\(\widehat {{A_4}}\)=32° (hai góc đồng vị)
• \(\widehat {{B_4}}\)=\(\widehat {{A_1}}\)=148° (hai góc đồng vị).
Vậy \(\widehat {{B_1}}\)=32°,\(\widehat {{B_2}}\)=148°,\(\widehat {{B_3}}\)=32°,\(\widehat {{B_4}}\)=148°.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 1 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 12 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 13 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 14 trang 89 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.