Giải bài 3.24 trang 44 SBT Toán 7 Kết nối tri thức tập 1
Cho hình 3.24.
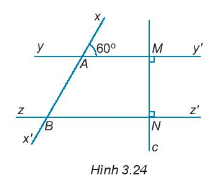
a) Giải thích tại sao \(yy'\parallel zz'\).
b) Tính số đo góc ABz.
c) Vẽ tia phân giác At của góc MAB, tia At cắt đường thẳng zz’ tại H. Tính số đo góc AHN.
Hướng dẫn giải chi tiết
Phương pháp giải:
a) Chỉ ra yy’ và zz’ cùng vuông góc với đường thẳng thứ 3
b)
-Tính góc ABH
-Tính góc ABz (kề bù góc ABH)
c)
-Tính góc BAM
-Tính góc AHB
-Tính góc AHN.
Lời giải chi tiết:

a)
Ta có: \(\left\{ \begin{array}{l}yy' \bot MN\\zz' \bot MN\end{array} \right. \Rightarrow yy'\parallel zz'\)
b)
Ta có: \(yy'\parallel zz' \Rightarrow \widehat {xAM} = \widehat {ABN} = {60^0}\) (hai góc đồng vị)
Mà \(\widehat {ABz} + \widehat {ABN} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ABz} + {60^0} = {180^0}\\ \Rightarrow \widehat {ABz} = {180^0} - {60^0}\\ \Rightarrow \widehat {ABz} = {120^0}\end{array}\)
c)
Ta có: \(yy'\parallel zz' \Rightarrow \widehat {ABz} = \widehat {BAM} = {120^0}\) (2 góc so le trong)
Mà tia phân giác At của góc MAB nên \(\widehat {BAH} = \widehat {HAM} = \dfrac{{\widehat {BAM}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\) (Tính chất tia phân giác của góc)
\(yy'\parallel zz' \Rightarrow \widehat {HAM} = \widehat {AHB} = {60^0}\) (2 góc so le trong)
Mặt khác: \(\widehat {AHB} + \widehat {AHN} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow {60^0} + \widehat {AHN} = {180^0}\\ \Rightarrow \widehat {AHN} = {180^0} - {60^0}\\ \Rightarrow \widehat {AHN} = {120^0}\end{array}\)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


