Giải bài 10 trang 69 SBT Toán 7 Cánh diều tập 2
Ở Hình 6 có \(\hat A = \hat B = 60^\circ \) và Cx là tia phân giác của góc ACy. Chứng minh Cx song song với AB.
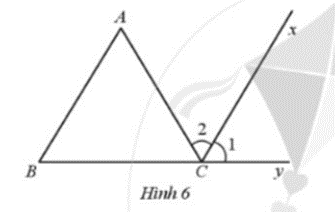
Hướng dẫn giải chi tiết bài 10
Phương pháp giải
Chứng minh: \(\widehat {B{}_1} = \widehat {{C_1}}\) suy ra Cx // AB (vì hai góc đồng vị bằng nhau)
Lời giải chi tiết
Vì \(\widehat {ACy}\) là góc ngoài của ∆ABC tại đỉnh C nên \(\widehat {ACy} = \hat A + \hat B\).
Do đó \(\widehat {ACy} = 60^\circ + 60^\circ = 120^\circ \)
Vì Cx là tia phân giác của góc ACy nên \({\hat C_1} = {\hat C_2} = \frac{{\widehat {ACy}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Suy ra \(\hat B = {\hat C_1}\) (cùng bằng 60°), mà chúng ở vị trí đồng vị nên Cx // AB.
Vậy Cx // AB.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.



