Giải bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác

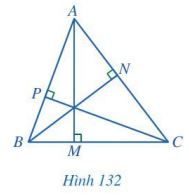
Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB (Hình 132).

Em có nhận xét gì về ba đường thẳng AM, BN, CP?

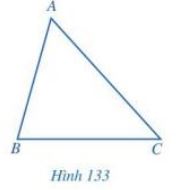
Cho tam giác ABC ( Hình 133). Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC.

Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.

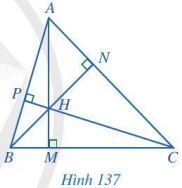
Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao đó có cùng đi qua một điểm hay không.

Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.

Cho tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng:

a) AH và BC;  

b) BH và CA;       

c) CH và AB.

Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:

a) Tam giác ABC nhọn;

b) Tam giác ABC vuông tại A;

c) Tam giác ABC có góc A tù.

Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc CA thì DC vuông góc với AB.

Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, \(\widehat {HCA} = 25^\circ \). Tính \(\widehat {BAC}\)và \(\widehat {HBA}\).

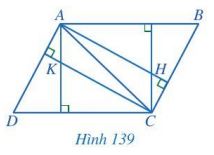
Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.

Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.

Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) H là giao điểm ba đường trung trực của tam giác ABC.

b) CH vuông góc với AB.

c) AH vuông góc với BC.

Cho tam giác ABC có AB > AC > BC và K là trực tâm. Trong các phát biểu sau, phát biểu nào đúng?

a) K là giao điểm ba đường trung trực của tam giác ABC.

b K là giao điểm ba đường cao của tam giác ABC.

c) K là giao điểm ba đường phân giác của tam giác ABC.

d) K là giao điểm ba đường trung tuyến của tam giác ABC.

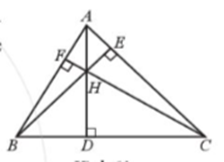
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.

Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.

Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Vẽ BE vuông góc với CD tại E. Gọi I là giao điểm của AC và BE; K là hình chiếu của I trên BC.

a) Chứng minh ba điểm D, I, K thẳng hàng.

b) Tìm điều kiện của tam giác ABC để I là trọng tâm của tam giác BCD.

Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Vẽ DE vuông góc với BC tại E.

a) Chứng minh trực tâm H của tam giác BAE nằm trên đường thẳng BD.

b) Chứng minh trực tâm của tam giác DAE nằm ngoài tam giác đó.

c) Tìm điều kiện của tam giác ABC để H cách đều các đỉnh của tam giác BAE.

Cho tam giác ABC cân tại A, đường trung tuyến AM. Từ M kẻ ME vuông góc với AB (E ∈ AB), kẻ MF vuông góc với AC (F ∈ AC). Gọi I là giao điểm của AM và EF. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh:

a) AM vuông góc với EF;

b) Trực tâm của các tam giác ABD và ACD nằm trên đường thẳng BC;

c) Trực tâm của các tam giác AEF, MEF, DBC và ABC nằm trên cùng một đường thẳng.