Nội dung bài học sẽ giới thiệu đến các em khái niệm và tính chất của Các trường hợp bằng nhau của tam giác vuông cùng với những dạng bài tập liên quan. Bên cạnh đó là những bài tập có hướng dẫn giải chi tiết sẽ giúp các em nắm được phương pháp giải các bài toán liên quan đề trường hợp bằng nhau của tam giác vuông.
Tóm tắt lý thuyết
1.1. Các trường hợp bằng nhau đã biết của hai tam giác vuông:
.png)
.png)
.png)
- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó bằng nhau (c.g.c; hình a).
- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc của tam giac vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g; hình b)
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g; hình c)
1.2. Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vùng đó bằng nhau (hình d).
Ví dụ 1: Cho tam giác ABC cân tại A, kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A.
Giải
.png)
Xét hai tam giác vuông ADB và ADC có AD cạnh chung
AB = AC (gt)
Nên \(\Delta ADB = \Delta ADC\) (cạnh huyền - cạnh góc vuông)
Suy ra \(\widehat {BAD} = \widehat {CAD}\) (góc tương ứng)
Vậy AD là tia phân giác của góc A.
Ví dụ 2: Cho tam giác ABC cân tại A, kẻ \(BH \bot AC,CK \bot AB.\) Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.
Giải
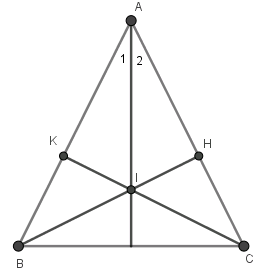
Xét hai tam giác AHB và AKC, ta có: AB=AC (gt)
\({B_1} = \widehat {{C_1}}\) (cùng nhau \(\frac{1}{2}\widehat B = \frac{1}{2}\widehat C\))
Nên \(\Delta AHB = \Delta AKC\) (cạnh huyền, cạnh góc nhọn) suy ra AH = AK (cạnh tương ứng)
Xét hai tam giác vuông AHI và AKI, ta có:
AI cạnh chung
AH= AK (CM trên)
Nên \(\Delta AHI = \Delta AKI\) (cạnh huyền, cạnh góc vuông)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\)
Vậy AI là tia phân giác của góc A.
Ví dụ 3: Cho \(\Delta ABC\) vuông tại A. Trên cạnh BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E.
a. So sánh độ dài AE và DE
b. Tia phân giác góc ngoài tại đỉnh C cắt đường thẳng BE ở K. Tính \(\widehat {BAK}.\)
Giải
.png)
a. Nối BE xét \(\Delta ABE\) và \(\Delta DBE,\) có:
\(\begin{array}{l}BAE = BDE = {90^0}\\BA = BD\,\,(gt)\end{array}\)
BC cạnh chung
Nên \(\Delta ABE = \Delta DBE\) (trường hợp cạnh huyền, cạnh góc vuông)
Suy ra AE = DE
b. Nối AK
Vì \(\Delta ABE = \Delta DBE\) nên ta có \(\widehat {ABE} = \widehat {DBE}\) hay BK là tia phân giác của góc B. Kẻ \(KM \bot BC,\,\,KN \bot AB,\,KH \bot AC.\)
Hai tam giác vuông KHC và KMC có cạnh huyền KC chung, hai góc nhọn bằng nhau \(\widehat {KCH} = \widehat {KCM}\) (CK là phân giác của \(\widehat {HCM}\)) nên \(\Delta KHC = \Delta KMC\)
Suy ra KH = KM
Tương tự \(\Delta KNB = \Delta KMB\) (cạnh huyền, góc nhọn)
Nên KM = KN
Suy ra KH = KN (cùng bằng KM)
Xét hai tam giác vuông KAH và KAN có:
KA cạnh chung
KH = KN
Nên \(\Delta KAH = \Delta KAN\) (cạnh huyền, cạnh góc vuông)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \frac{1}{2}\widehat {HAN} = {45^0}\)
Do đó
\(\begin{array}{l}\widehat {BAK} = \widehat {BAC} + \widehat {{A_2}}\\ = {90^0} + {45^0}\end{array}\)
Vậy \(\widehat {BAK} = {135^0}\)
Bài tập minh họa
Bài 1: Cho \(\Delta ABC\) vuông tại A (AB < AC), M là một điểm thuộc cạnh AC. Kẻ MH vuông góc với BC \((H \in BC)\). Biết MH = HB. Chứng minh rằng AH là tia phân giác của góc A.
Giải
.png)
Kẻ \(HI \bot AB,\,\,HK \bot AC\,\,(I \in AB,\,K \in AC)\)
Ta có \(\widehat {{M_1}} = \widehat B\) (Vì \(\widehat {{M_1}} + \widehat C = {90^0};\widehat B + \widehat C = {90^0}\,\))
Xét \(\Delta HIB\) và \(\Delta HKM\)
Có: \(\widehat I = \widehat K = {90^0}\)
HB=MH (gt)
\(\widehat B = \widehat {{M_1}}\)
Vậy \(\Delta HIB = \Delta HKM\) (cạnh huyền, góc nhọn)
Suy ra HI = HK
Xét \(\Delta AIH = \Delta AKH\) có:
\(\widehat I = \widehat K = {90^0}\)
AH cạnh chung
HI = HK
Vậy \(\Delta AIH = \Delta AKH\) (cạnh huyền, cạnh góc vuông)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\)
Vậy AH là tia phân giác của góc A.
Bài 2: Cho tam giác cân ABC, cạnh đáy BC. Từ B kẻ đường vuông góc với AB và từ C kẻ đường vuông góc với AC. Hai đường này cắt nhau tại M. Chứng minh rằng:
a. \(\Delta ABM = \Delta ACM\)
b. AM là đường trung trực của BC.
Giải
.png)
a. Xét hai tam giác vuông ABM và ACM có:
Cạnh huyền AM chung
AB = AC (gt)
Vậy \(\Delta ABM = \Delta ACM\) (cạnh huyền, cạnh góc vuông)
b. Gọi H là giao điểm của AM và BC, hai tam giác AHB và AHC có AB = AC (gt), \(\widehat {{A_1}} = \widehat {{A_2}}\,\,(\Delta ABM = \Delta ACM);\)AH là cạnh chung. Nên \(\Delta AHB = \Delta AHC\,\,(c.g.c)\)
Suy ra \(HB = HC;\,\,\,\widehat {{H_1}} = \widehat {{H_2}}\)
Mà \(\,\,\widehat {{H_1}} = \widehat {{H_2}} = {180^0}\)
Nên \(\,\,\widehat {{H_1}} = \widehat {{H_2}} = {90^0}\)hay \(AH \bot BC.\)
Vậy AM là đường trung trực của BC (\(AH \bot BC\) và \(HB = HC\))
Bài 3: Cho \(\Delta ABC\) vuông tại A. Ở miền ngoài tam giác vẽ các tam giác vuông cân ABD, ACF (AB =BD; AC = CF).
a. Chứng minh D, A, F thẳng hàng.
b. Từ D và F hạ các đường vuông góc DD’, FF’ xuống đường thẳng BC. Chứng minh: DD’ + FF’ = BC.
Giải
a. Vì các tam giác DBA, ACF vuông cân nên ta suy ra:
\(\widehat {DAB} = {45^0};\widehat {{\rm{CAF}}} = {45^0}\)
Nên
\(\begin{array}{l}\widehat {{\rm{DAF}}} = \widehat {{\rm{DAB}}} + \widehat {{\rm{BAC}}} + \widehat {{\rm{CAF}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{45^0} + {90^0} + {45^0} = {180^0}\end{array}\)
Vậy D, A, F thẳng hàng
b. Từ A vẽ \(AH \bot BC\)
Xét hai tam giác vuông DD’B và BHA có:
BD=AB (gt)
\(\widehat {DBD'} = \widehat {BAH}\) (Cùng phụ với \(\widehat {ABH}\))
Nên \(\Delta DBD' = \Delta BAH\) (cạnh huyền, góc nhọn)
.png)
Suy ra DD’ = BH (1)
Tương tự \(\Delta F'CF = \Delta HAC\) (cạnh huyền, góc nhọn)
Suy ra FF’=HC (2)
Cộng vế với vế (1) và (2) ta có:
DD’+ FF’=BH + HC
Vậy DD’ + FF’ = BC.
3. Luyện tập Bài 8 Chương 2 Hình học 7
Qua bài giảng Các trường hợp bằng nhau của tam giác vuông này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nhận biết được các trường hợp bằng nhau đã biết của hai tam giác vuông
- Trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
3.1. Trắc nghiệm về Định lí Pi-ta-go
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 7 Bài 8 cực hay có đáp án và lời giải chi tiết.
-
- A. BA = PM
- B. BA = PN
- C. CA = MN
- D. \(\widehat A = \widehat N\)
-
- A. AC = MP
- B. AB = MN
- C. BC= NP
- D. AC = MN
-
- A. \(\Delta ABC = \Delta F{\rm{ED}}\,\,\)
- B. \(\Delta ABC = \Delta F{\rm{DE}}\,\,\)
- C. \(\Delta BAC = \Delta F{\rm{ED}}\,\,\)
- D. \(\Delta ABC = \Delta D{\rm{EF}}\,\,\)
Câu 4-9: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK về Định lí Pi-ta-go
Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 7 Bài 8 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 63 trang 136 SGK Toán 7 Tập 1
Bài tập 64 trang 136 SGK Toán 7 Tập 1
Bài tập 65 trang 137 SGK Toán 7 Tập 1
Bài tập 66 trang 137 SGK Toán 7 Tập 1
Bài tập 93 trang 151 SBT Toán 7 Tập 1
Bài tập 94 trang 151 SBT Toán 7 Tập 1
Bài tập 95 trang 151 SBT Toán 7 Tập 1
Bài tập 96 trang 151 SBT Toán 7 Tập 1
Bài tập 97 trang 151 SBT Toán 7 Tập 1
Bài tập 98 trang 151 SBT Toán 7 Tập 1
Bài tập 99 trang 151 SBT Toán 7 Tập 1
Bài tập 100 trang 151 SBT Toán 7 Tập 1
Bài tập 101 trang 151 SBT Toán 7 Tập 1
4. Hỏi đáp Bài 8 Chương 2 Hình học 7
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 7 HỌC247









