Hoạt động 5 trang 26 SGK Toán 11 Kết nối tri thức tập 1
Cho hàm số y = cos x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cos x trên đoạn [– π; π] bằng cách tính giá trị của cos x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của cos x với những x âm.

Bằng cách lấy nhiều điểm M(x; cos x) với x ∈ [– π; π] và nối lại ta được đồ thị hàm số y = cos x trên đoạn [– π; π].
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kì T = 2π, ta được đồ thị của hàm số y = cos x như hình dưới đây.
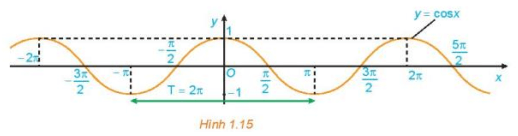
Từ đồ thị ở Hình 1.15, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số y = cos x.
Hướng dẫn giải chi tiết Hoạt động 5
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Hàm số y = f(x) = cos x có tập xác định là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cos (– x) = cos x = f(x), ∀ x ∈ D.
Vậy y = cos x là hàm số chẵn.
b) Ta có: cos 0 = 1, \(\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}, \)\(\cos \frac{\pi }{2} = 0,\, \)\(\cos \frac{{3\pi }}{4} = - \frac{{\sqrt 2 }}{2}\), cos π = – 1.
Vì y = cos x là hàm số chẵn nên \(\cos \left( { - \frac{\pi }{4}} \right) = \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\), \(\cos \left( { - \frac{\pi }{2}} \right) = \cos \frac{\pi }{2} = 0\), \(\cos \left( { - \frac{{3\pi }}{4}} \right) = \cos \frac{{3\pi }}{4} = - \frac{{\sqrt 2 }}{2}\), cos(– π) = cos π = – 1.
Vậy ta hoàn thành được bảng như sau:

c) Quan sát Hình 1.15, ta thấy đồ thị hàm số y = cos x có:
+) Tập giá trị là [– 1; 1];
+) Đồng biến trên mỗi khoảng (−π+k2π;k2π) (do đồ thị hàm số đi lên từ trái sang phải trên mỗi khoảng này) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\,\pi + k2\pi } \right),\,k \in Z\) (do đồ thị hàm số đi xuống từ trái sang phải trên mỗi khoảng này).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Luyện tập 4 trang 26 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Vận dụng 1 trang 26 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 5 trang 27 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Vận dụng 2 trang 27 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 6 trang 28 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 6 trang 29 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 7 trang 29 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 7 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.15 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.16 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.17 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.18 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 1.19 trang 30 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Bài tập 1.16 trang 17 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.17 trang 17 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.18 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.19 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.20 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.21 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.22 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.23 trang 18 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 1.24 trang 19 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





