Giải Bài 8 trang 82 SGK Toán 11 Chân trời sáng tạo tập 2

Tính thể tích của khối chóp cụt lục giác đều \(ABCDEF.{\rm{ }}A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\).

QUẢNG CÁO

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).

Lời giải chi tiết

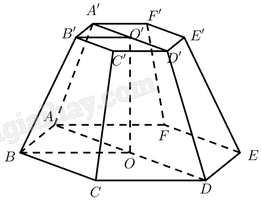
Diện tích đáy lớn là: \(S = 6{S_{ABO}} = 6.\frac{{A{B^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{2}\)

Diện tích đáy bé là: \(S' = 6{S_{A'B'O'}} = 6.\frac{{A'B{'^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{8}\)

Thể tích khối chóp cụt lục giác đều là:

\(V = \frac{1}{3}.a\left( {\frac{{3{a^2}\sqrt 3 }}{2} + \sqrt {\frac{{3{a^2}\sqrt 3 }}{2}.\frac{{3{a^2}\sqrt 3 }}{8}} + \frac{{3{a^2}\sqrt 3 }}{8}} \right) = \frac{{3{a^3}\sqrt 3 }}{8}\)

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Giải Bài 8 trang 82 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST HAY thì click chia sẻ