Bài tập 6 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = \(a\sqrt{3}\), đáy ABCD là hình thang vuông tại A và B có AB = a, AD = 3a, BC = a. Tính thể tích khối chóp S.BCD theo a?
Hướng dẫn giải chi tiết Bài tập 6
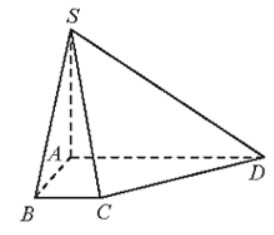
Ta có: .
Lại có: .
Suy ra .
Vậy .
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 8 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 9 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 10 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





