Bài tập 3 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho hình lập phương cạnh a. Gọi M, N lần lượt là trung điểm của AC và . Tính khoảng cách giữa hai đường thẳng MN và ?
Hướng dẫn giải chi tiết Bài tập 3
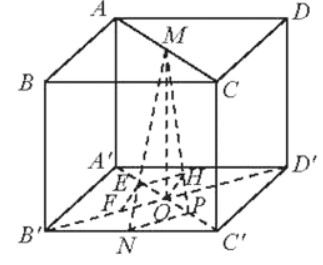
Ta có: B'D' A'C' tại O.
Gọi P là trung điểm của OC'.
Vě OH ⊥ MP, HE // NP, EF // OH.
ABCD là hình lập phương, ta dễ dàng có được: B'D' ⊥ (A'C'CA).
Hay B'D' ⊥ OH, mà OH // EF.
EF ⊥ B'D' (1).
NP // B'D' NP ⊥ (A'C'CA) hay NP ⊥ OH.
Đồng thời OH ⊥ MP.
OH ⊥ (MNP) hay OH ⊥ MN EF ⊥ MN (2)
Từ (1) và (2) ta có: d(MN, B'D') = EF = OH.
Xét tam giác vuông MOP, ta có OM = a, OP = , suy ra OH = .
Vậy d(MN, B'D') = .
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 8 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 9 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 10 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


