HÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo ChÆ°ÆĄng 4 Bà i 4 Hai máš·t phášģng song song mÃīn ToÃĄn láŧp 11 giÚp cÃĄc em háŧc sinh nášŊm váŧŊng phÆ°ÆĄng phÃĄp giášĢi bà i tášp và Ãīn luyáŧn táŧt kiášŋn tháŧĐc.
-
Hoᚥt Äáŧng kháŧi Äáŧng trang 113 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Báŧ máš·t trÊn cáŧ§a máŧi bášc thang nà y ÄÆ°áŧĢc Äáš·t nhÆ° thášŋ nà o so váŧi máš·t ÄášĨt?

-
Hoᚥt Äáŧng khÃĄm phÃĄ 1 trang 113 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
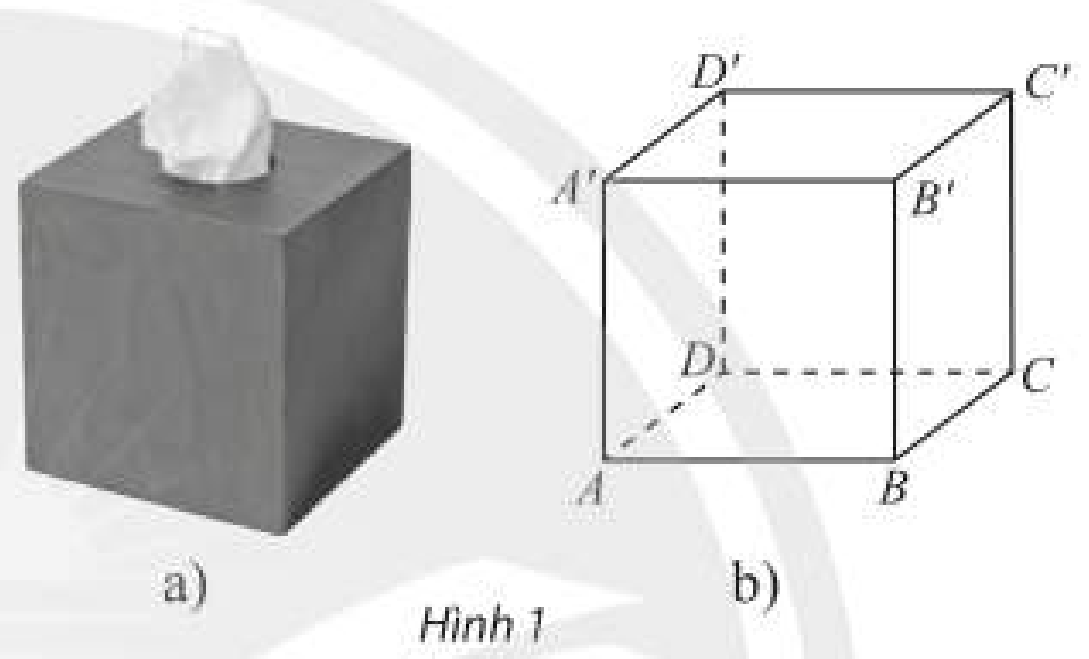
Háŧp giášĨy cÃģ cÃĄc máš·t là hÃŽnh vuÃīng áŧ HÃŽnh 1a ÄÆ°áŧĢc váš― lᚥi váŧi cÃĄc Äáŧnh là \(A,B,C,D,A',B',C',D'\) nhÆ° HÃŽnh 1b. Gáŧi tÊn cáš·p máš·t phášģng:
a) CÃģ ba Äiáŧm chung khÃīng thášģng hà ng.
b) Là hai máš·t phášģng phÃĒn biáŧt và cÃģ máŧt Äiáŧm chung.
c) KhÃīng cÃģ bášĨt kÃŽ Äiáŧm chung nà o.
-
Vášn dáŧĨng 1 trang 114 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
TÃŽm phášģng song song cÃģ trong hÃŽnh cháŧĨp cÄn phÃēng áŧ HÃŽnh 4.

-
Hoᚥt Äáŧng khÃĄm phÃĄ 2 trang 114 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
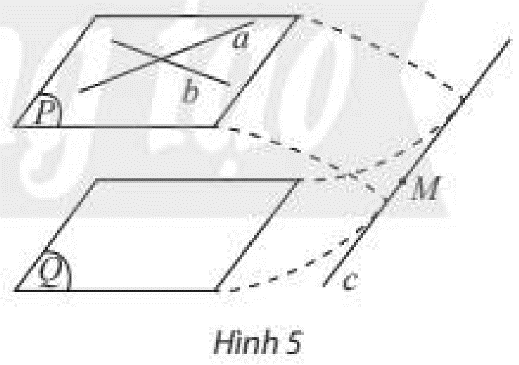
Cho máš·t phášģng \(\left( P \right)\) cháŧĐa hai ÄÆ°áŧng thášģng \(a,b\) cášŊt nhau và cÃđng song song váŧi máš·t phášģng \(\left( Q \right)\). GiášĢ sáŧ \(\left( P \right)\) và \(\left( Q \right)\) cÃģ Äiáŧm chung \(M\) thÃŽ \(\left( P \right)\) cášŊt \(\left( Q \right)\) theo giao tuyášŋn \(c\) (HÃŽnh 5).
a) GiášĢi thÃch tᚥi sao ÄÆ°áŧng thášģng \(c\) phášĢi cášŊt Ãt nhášĨt máŧt trong hai ÄÆ°áŧng thášģng \(a,b\). Äiáŧu nà y cÃģ trÃĄi váŧi giášĢ thiášŋt \(a\) và \(b\) cÃđng song song váŧi \(\left( Q \right)\) khÃīng?
b) RÚt ra kášŋt luášn váŧ sáŧ Äiáŧm chung và váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a \(\left( P \right)\) và \(\left( Q \right)\).
- VIDEOYOMEDIA
-
Tháŧąc hà nh 1 trang 115 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho táŧĐ diáŧn \(ABCD\) cÃģ \(E,F,H\)lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a \(AB,AC,AD\). CháŧĐng minh \(\left( {EFH} \right)\parallel \left( {BCD} \right)\).
-
Hoᚥt Äáŧng khÃĄm phÃĄ 3 trang 115 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
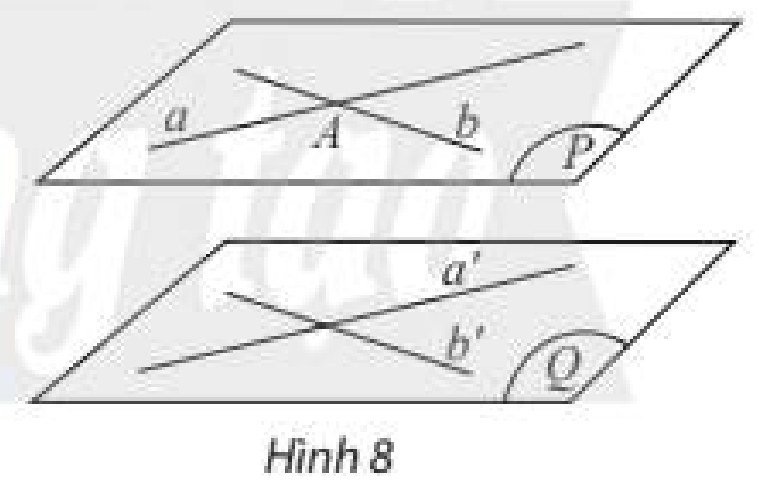
a) Cho Äiáŧm \(A\) áŧ ngoà i máš·t phášģng \(\left( Q \right)\). Trong \(\left( Q \right)\) váš― hai ÄÆ°áŧng thášģng cášŊt nhau \(a'\) và \(b'\). Là m thášŋ nà o Äáŧ váš― hai ÄÆ°áŧng thášģng \(a\) và \(b\) Äi qua \(A\) và song song váŧi \(\left( Q \right)\)?
b) CÃģ nhášn xÃĐt gÃŽ váŧ máŧi liÊn háŧ giáŧŊa \(mp\left( {a,b} \right)\)và \(\left( Q \right)\)?
-
Hoᚥt Äáŧng khÃĄm phÃĄ 4 trang 115 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
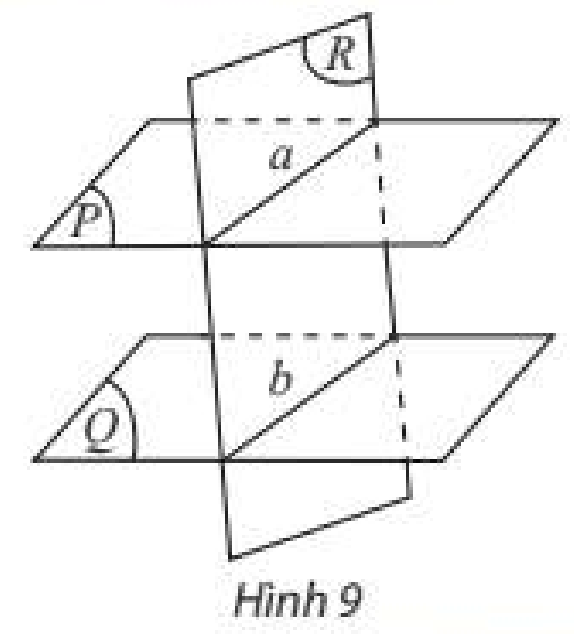
Cho ba máš·t phášģng \(\left( P \right),\left( Q \right),\left( R \right)\) thoášĢ mÃĢn \(\left( P \right)\parallel \left( Q \right)\), \(\left( R \right) \cap \left( P \right) = a\) và \(\left( R \right) \cap \left( Q \right) = b\). XÃĐt váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a \(a\) và \(b\).
-
Tháŧąc hà nh 2 trang 116 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hÃŽnh chÃģp \(S.ABCD\) váŧi ÄÃĄy \(ABCD\) là hÃŽnh bÃŽnh hà nh cÃģ \(O\) là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo, tam giÃĄc \(SBD\) là tam giÃĄc Äáŧu. Máŧt máš·t phášģng \(\left( \alpha \right)\) di Äáŧng song song váŧi máš·t phášģng \(\left( {SBD} \right)\) và cášŊt Äoᚥn thášģng \(AC\). CháŧĐng minh cÃĄc giao tuyášŋn cáŧ§a \(\left( \alpha \right)\) váŧi hÃŽnh chÃģp tᚥo thà nh máŧt tam giÃĄc Äáŧu.
-
Vášn dáŧĨng 2 trang 116 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
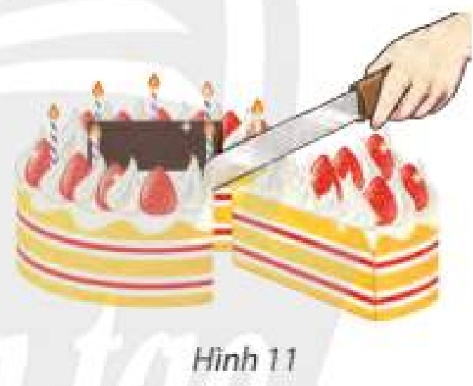
Khi dÃđng dao cášŊt cÃĄc láŧp bÃĄnh (HÃŽnh 11), giášĢ sáŧ báŧ máš·t cáŧ§a cÃĄc láŧp bÃĄnh là cÃĄc máš·t phášģng song song và con dao ÄÆ°áŧĢc xem nhÆ° máš·t phášģng \(\left( P \right)\), nÊu kášŋt luášn váŧ cÃĄc giao tuyášŋn tᚥo báŧi \(\left( P \right)\) váŧi cÃĄc báŧ máš·t cáŧ§a cÃĄc láŧp bÃĄnh. GiášĢi thÃch.
-
Hoᚥt Äáŧng khÃĄm phÃĄ 5 trang 116 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho ÄÆ°áŧng thášģng \(a\) song song váŧi máš·t phášģng \(\left( P \right)\), máš·t phášģng \(\left( Q \right)\) cháŧĐa \(a\) và cášŊt \(\left( P \right)\) theo giao tuyášŋn \(b\) (HÃŽnh 10). Trong \(\left( Q \right)\), hai ÄÆ°áŧng thášģng \(a,b\) cÃģ bao nhiáŧu Äiáŧm chung?
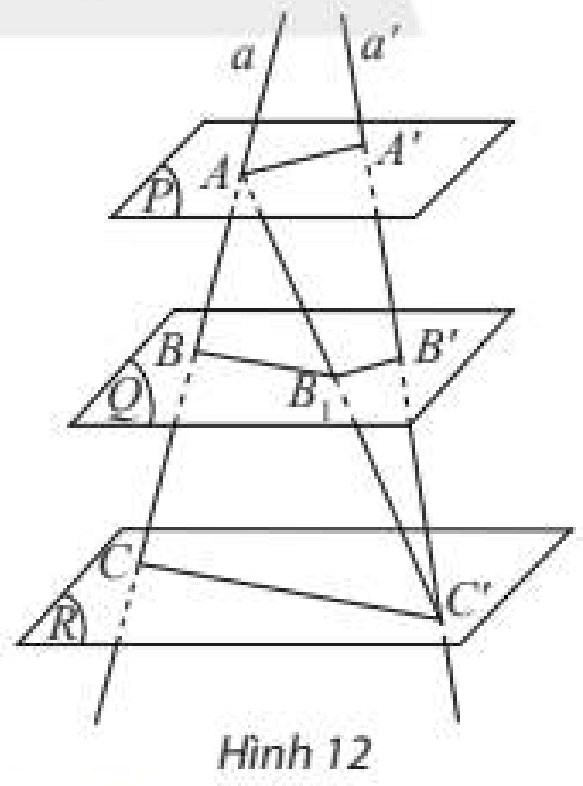
Cho ba máš·t phášģng song song \(\left( P \right),\left( Q \right),\left( R \right)\) lᚧn lÆ°áŧĢt cášŊt hai ÄÆ°áŧng thÄng \(a\) và \(a'\) tᚥi cÃĄc Äiáŧm \(A,B,C\) và \(A',B',C'\). Gáŧi \({B_1}\) là giao Äiáŧm cáŧ§a \(AC'\) váŧi \(\left( Q \right)\) (HÃŽnh 12).
a) Trong tam giÃĄc \(ACC'\), cÃģ nhášn xÃĐt gÃŽ váŧ máŧi liÊn háŧ giáŧŊa \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C'}}\)?
b) Trong tam giÃĄc \(AA'C'\), cÃģ nhášn xÃĐt gÃŽ váŧ máŧi liÊn háŧ giáŧŊa \(\frac{{A{B_1}}}{{{B_1}C'}}\) và \(\frac{{A'B'}}{{B'C'}}\)?
c) TáŧŦ ÄÃģ, nášŋu nhášn xÃĐt váŧ máŧi liÊn háŧ giáŧŊa cÃĄc táŧ sáŧ \(\frac{{AB}}{{A'B'}},\frac{{BC}}{{B'C'}},\frac{{AC}}{{A'C'}}\).
-
Tháŧąc hà nh 3 trang 117 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hÃŽnh chÃģp \(S.ABC\) cÃģ \(SA = 9,SB = 12,SC = 15\). TrÊn cᚥnh \(SA\) lášĨy cÃĄc Äiáŧm \(M,N\) sao cho \(SM = 4,MN = 3,N4 = 2\). Váš― hai máš·t phášģng song song váŧi máš·t phášģng \(\left( {ABC} \right)\), lᚧn lÆ°áŧĢt Äi qua \(M,N\), cášŊt \(SB\) theo tháŧĐ táŧą tᚥi \(M',N'\) và cášŊt \(SC\) theo tháŧĐ táŧą tᚥi \(M'',N''\). TÃnh Äáŧ dà i cÃĄc Äoᚥn thášģng \(SM',M'N',{\rm{ }}M''N'',N''C\).
-
Hoᚥt Äáŧng khÃĄm phÃĄ 6 trang 117 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
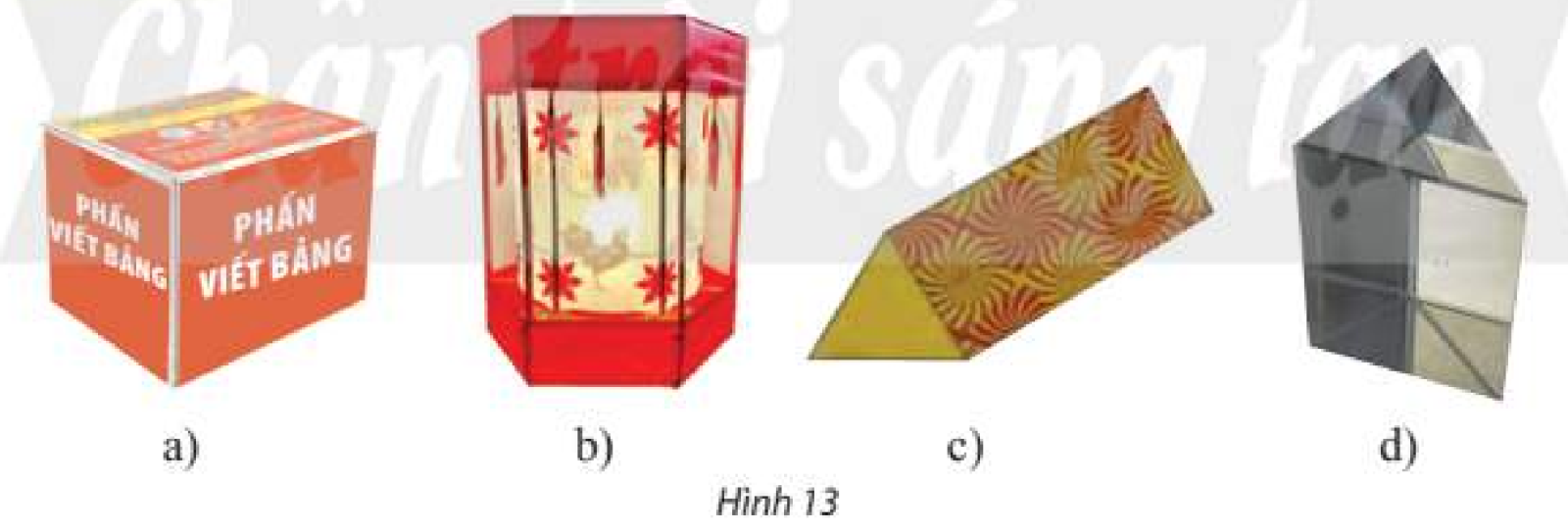
HÃŽnh dᚥng cáŧ§a cÃĄc ÄÃī vášt nhÆ° háŧp phÃĒn, láŧng ÄÃĻn, háŧp quà , lÄng kÃnh cÃģ Äáš·c Äiáŧm gÃŽ giáŧng nhau?
-
Hoᚥt Äáŧng khÃĄm phÃĄ 7 trang 118 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hÃŽnh lÄng tráŧĨ \(ABCD.A'B'C'D'\) cÃģ ÄÃĄy \(ABCD\) là hÃŽnh bÃŽnh hà nh. CháŧĐng minh rášąng:
a) Báŧn máš·t bÊn và máš·t ÄÃĄy cÃēn lᚥi cáŧ§a hÃŽnh lÄng tráŧĨ là cÃĄc hÃŽnh bÃŽnh hà nh;
b) CÃĄc máš·t \(AA'C'C\) và \(BB'D'D\)là hÃŽnh bÃŽnh hà nh
c) Báŧn Äoᚥn thášģng \(A'C,AC',B'D,BD\) cÃģ cÃđng trung Äiáŧm.
-
Tháŧąc hà nh 4 trang 119 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
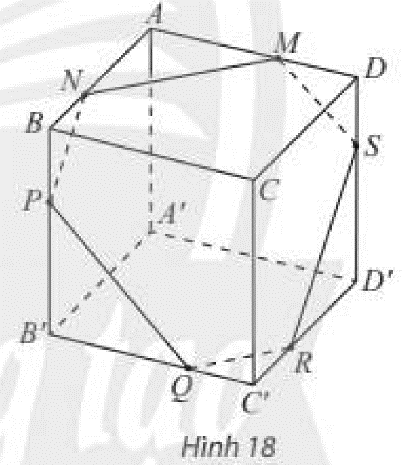
Cho hÃŽnh háŧp \(ABCD.A'B'C'D'\) và máŧt máš·t phášģng \(\left( \alpha \right)\) cášŊt cÃĄc máš·t cáŧ§a hÃŽnh háŧp theo cÃĄc giao tuyášŋn \(MN,NP,PQ{\rm{,}}QR,RS,SM\) nhÆ° HÃŽnh 18. CháŧĐng minh cÃĄc cáš·p cᚥnh Äáŧi cáŧ§a láŧĨc giÃĄc \(MNPQRS\) song song váŧi nhau.
-
Vášn dáŧĨng 3 trang 119 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
TÃŽm hÃŽnh lÄng tráŧĨ cÃģ tháŧ lášĨy máŧt máš·t bášĨt kÃŽ là m máš·t ÄÃĄy.
-
GiášĢi Bà i 1 trang 119 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Trong máš·t phášģng \(\left( P \right)\) cho hÃŽnh bÃŽnh hà nh \(ABCD\). Ta dáŧąng cÃĄc náŧa ÄÆ°áŧng thášģng song song váŧi nhau và nášąm váŧ máŧt phÃa Äáŧi váŧi \(\left( P \right)\) lᚧn lÆ°áŧĢt Äi qua cÃĄc Äiáŧm \(A,B,C,D\). Máŧt máš·t phášģng \(\left( Q \right)\) cášŊt báŧn náŧa ÄÆ°áŧng thášģng nÃģi trÊn tᚥi \(A',B',C',D'\). CháŧĐng minh rášąng:
\(AA' + CC' = BB' + DD'\).
-
GiášĢi Bà i 2 trang 120 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hÃŽnh chÃģp \(S.ABCD\), ÄÃĄy \(ABCD\) là hÃŽnh bÃŽnh hà nh cÃģ \(O\) là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo. Gáŧi \(M,N\) lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a \(SA,SD\).
a) CháŧĐng minh rášąng \(\left( {OMN} \right)\parallel \left( {SBC} \right)\).
b) Gáŧi \(E\) là trung Äiáŧm cáŧ§a \(AB\) và \(F\) là máŧt Äiáŧm thuáŧc \(ON\). CháŧĐng minh \(EF\) song song váŧi \(\left( {SBC} \right)\).
-
GiášĢi Bà i 3 trang 120 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hai hÃŽnh vuÃīng \(ABCD\) và \(ABEF\) áŧ trong hai máš·t phášģng khÃĄc nhau. TrÊn cÃĄc ÄÆ°áŧng chÃĐo \(AC\) và \(BF\) lᚧn lÆ°áŧĢt lášĨy cÃĄc Äiáŧm \(M,N\) sao cho \(AM = BN\). CÃĄc ÄÆ°áŧng thášģng song song váŧi \(AB\) váš― táŧŦ \(M,N\) lᚧn lÆ°áŧĢt cášŊt \(AD,AF\) tᚥi \(M',N'\).
a) CháŧĐng minh \(\left( {CBE} \right)\parallel \left( {ADF} \right)\).
b) CháŧĐng minh \(\left( {DEF} \right)\parallel \left( {MNN'M'} \right)\).
-
GiášĢi Bà i 4 trang 120 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cho hÃŽnh háŧp \(ABCD.A'B'C'D'\). Gáŧi \({G_1}\) và \({G_2}\) lᚧn lÆ°áŧĢt là tráŧng tÃĒm cáŧ§a hai tam giÃĄc \(BDA'\) và \(B'D'C\). CháŧĐng minh \({G_1}\) và \({G_2}\) chia Äoᚥn \(AC\) thà nh ba phᚧn bášąng nhau.
-
GiášĢi Bà i 5 trang 120 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Äáŧ là m máŧt khung láŧng ÄÃĻn kÃĐo quÃĒn hÃŽnh lÄng tráŧĨ láŧĨc giÃĄc\(ABCDEF.A'B'C'D'E'F'\), BÃŽnh gášŊn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song váŧi máš·t phášģng ÄÃĄy và cášŊt nhau tᚥi \({O_1}\) (HÃŽnh 19).
a) XÃĄc Äáŧnh giao tuyášŋn cáŧ§a \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) váŧi cÃĄc máš·t bÊn cáŧ§a lÄng tráŧĨ.
b) Cho biášŋt \(A'{A_1} = 6A{A_1}\) và \(AA' = 70{\rm{ }}cm\). TÃnh \(C{C_1}\) và \({C_1}C'\).
-
GiášĢi Bà i 6 trang 120 SGK ToÃĄn 11 ChÃĒn tráŧi sÃĄng tᚥo tášp 1 - CTST
Cháŧ ra cÃĄc máš·t phášģng song song trong máŧi hÃŽnh sau. TÃŽm thÊm máŧt sáŧ và dáŧĨ khÃĄc váŧ cÃĄc máš·t phášģng song song trong tháŧąc tášŋ.

-
Bà i tášp 1 trang 127 SBT ToaĖn 11 TÃĒĖĢp 1 ChÃĒn tráŧi sÃĄng tᚥo - CTST
Cho hÃŽnh chÃģp S.ABCD cÃģ ÄÃĄy là hÃŽnh thang ABCD, AD // BC, AD = 2BC. Gáŧi E, F, I lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a cÃĄc cᚥnh SA, AD, SD.
a) CháŧĐng minh: (BEF) // (SCD) và CI // (BEF).
b) TÃŽm giao tuyášŋn cáŧ§a hai máš·t phášģng (SBC) và (SAD).
c) TÃŽm giao Äiáŧm K cáŧ§a FI váŧi giao tuyášŋn váŧŦa tÃŽm ÄÆ°áŧĢc áŧ cÃĒu b, táŧŦ ÄÃģ cháŧĐng minh (SBF) // (KCD).
-
Bà i tášp 2 trang 127 SBT ToaĖn 11 TÃĒĖĢp 1 ChÃĒn tráŧi sÃĄng tᚥo - CTST
Cho hÃŽnh chÃģp S.ABCD cÃģ ÄÃĄy là hÃŽnh bÃŽnh hà nh tÃĒm O. Gáŧi M, N lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a SA và CD.
a) CháŧĐng minh (OMN) // (SBC).
b) GiášĢ sáŧ hai tam giÃĄc SAD và SAB là cÃĄc tam giÃĄc cÃĒn tᚥi A. Gáŧi AE và AF lᚧn lÆ°áŧĢt là ÄÆ°áŧng phÃĒn giÃĄc trong cáŧ§a hai tam giÃĄc SAD và SAB. CháŧĐng minh EF // (SBD).
-
Bà i tášp 3 trang 128 SBT ToaĖn 11 TÃĒĖĢp 1 - CTST ChÃĒn tráŧi sÃĄng tᚥo
Cho hÃŽnh háŧp ABCD.AâBâCâDâ. CháŧĐng minh:
a) (BDAâ) // (BâDâC).
b) ÄÆ°áŧng chÃĐo ACâ Äi qua tráŧng tÃĒm G và Gâ cáŧ§a hai tam giÃĄc BDAâ và BâDâC.
c) G và Gâ chia Äoᚥn ACâ thà nh ba phᚧn bášąng nhau.
-
Bà i tášp 4 trang 128 SBT ToaĖn 11 TÃĒĖĢp 1 ChÃĒn tráŧi sÃĄng tᚥo - CTST
Cho hÃŽnh chÃģp S.ABCD cÃģ ÄÃĄy ABCD là hÃŽnh bÃŽnh hà nh và M, N lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a AB, CD. (P) là máš·t phášģng Äi qua MN và song song váŧi máš·t phášģng (SAD). TÃŽm giao tuyášŋn cáŧ§a cÃĄc máš·t cáŧ§a hÃŽnh chÃģp váŧi máš·t phášģng (P)?


