Thực hành 2 trang 116 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải:

‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.

‒ Sử dụng định lí Thales trong tam giác.

Lời giải chi tiết:

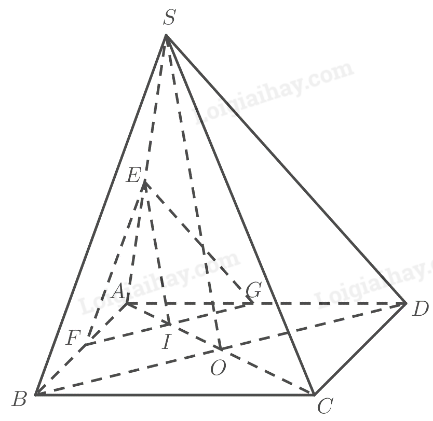
TH1: \(\left( \alpha \right)\) cắt đoạn \(AO\) tại \(I\).

Gọi \(E,F,G\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SA,AB,AD\).

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = FG\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow FG\parallel B{\rm{D}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{AG}}{{AD}} = \frac{{FG}}{{B{\rm{D}}}}\left( 1 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = EF\\\left( {SAB} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow EF\parallel SB \Rightarrow \frac{{AF}}{{AB}} = \frac{{AE}}{{AS}} = \frac{{EF}}{{SB}}\left( 2 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAD} \right) = EG\\\left( {SAD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow EG\parallel SD \Rightarrow \frac{{AG}}{{AD}} = \frac{{AE}}{{AS}} = \frac{{EG}}{{SD}}\left( 3 \right)\end{array}\)

Từ (1), (2) và (3) suy ra \(\frac{{EF}}{{SB}} = \frac{{EG}}{{S{\rm{D}}}} = \frac{{FG}}{{B{\rm{D}}}}\).

Tam giác \(SBD\) đều nên \(SB = SD = BD\).

Do đó \(EF = EG = FG\). Vậy tam giác \(EFG\) đều.

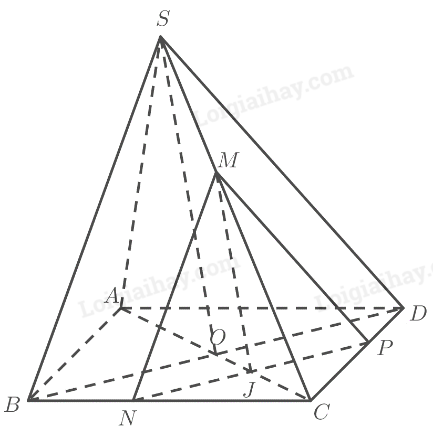
TH2: \(\left( \alpha \right)\) cắt đoạn \(CO\) tại \(J\).

Gọi \(M,N,P\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SC,BC,C{\rm{D}}\).

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = NP\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow NP\parallel B{\rm{D}} \Rightarrow \frac{{CN}}{{CB}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\left( 4 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SBC} \right) = MN\\\left( {SBC} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow MN\parallel SB \Rightarrow \frac{{CM}}{{C{\rm{S}}}} = \frac{{CN}}{{CB}} = \frac{{MN}}{{SB}}\left( 5 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SCD} \right) = MP\\\left( {SCD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow MP\parallel SD \Rightarrow \frac{{C{\rm{M}}}}{{C{\rm{S}}}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{MP}}{{SD}}\left( 6 \right)\end{array}\)

Từ (4), (5) và (6) suy ra \(\frac{{MN}}{{SB}} = \frac{{MP}}{{S{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\).

Tam giác \(SBD\) đều nên \(SB = SD = BD\).

Do đó \(MN = MP = NP\). Vậy tam giác \(MNP\) đều.

-- Mod Toán 11 HỌC247