Phần hướng dẫn giải bài tập SGK bài Ôn tập cuối năm Hình học 11 sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập Ôn tập cuối năm từ SGK Hình học 11 Cơ bản và Nâng cao.
-
Bài tập 5 trang 200 SBT Hình học 11
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, \(AB = a\sqrt 3 ,\widehat {BAD} = {120^0}\). Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30o. Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)
-
Bài tập 6 trang 200 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
-
Bài tập 7 trang 200 SBT Hình học 11
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên AA' = \(a\sqrt 2 \). Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C.
-
Bài tập 8 trang 200 SBT Hình học 11
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a. Gọi E là điểm đối xứng của D qua trung điểm SA, M là trung điểm của AE, N là trung điểm của BC. Chứng minh rẳng MN vuông góc với BD và tính khoảng cách giữa hai đường thẳng MN và AC.
- VIDEOYOMEDIA
-
Bài tập 9 trang 200 SBT Hình học 11
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABC). Gọi M là trung điểm của AB, mặt phẳng qua SM song song với BC cắt AC tại N. Biết góc tạo bởi (SBC) và (ABC) là 60o. Tìm khoảng cách giữa hai đường thẳng AB và SN.
-
Bài tập 1 trang 124 SGK Hình học 11 NC
Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.
a. Xét bốn tam giác APN, PBM, NMC, MNP. Tìm phép dời hình biến tam giác APN lần lượt thành một trong ba tam giác còn lại.
b. Phép vị tự nào biến tam giác ABC thành tam giác MNP ?
c. Xét tam giác có ba đỉnh là trực tâm của ba tam giác APN, PBM và NCM. Chứng tỏ rằng tam giác đó bằng tam giác APN. Chứng minh điều đó cũng đúng nếu thay trực tâm bằng trọng tâm, hoặc tâm đường tròn ngoại tiếp hoặc tâm đường tròn nội tiếp.
-
Bài tập 2 trang 124 SGK Hình học 11 NC
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
a. Gọi I là giao điểm của MP và NQ. Phép đối xứng tâm ĐI biến các đường thẳng MM’, NN’, PP’, QQ’ thành những đường thẳng nào ?
b. Chứng tỏ rằng bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại một điểm. Nhận xét gì về vị trí điểm đồng quy và hai điểm I, O ?
-
Bài tập 3 trang 125 SGK Hình học 11 NC
Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.
a. Xác định phép quay biến tam giác ABQ thành tam giác ANC.
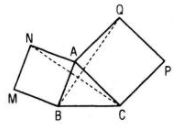
b. Chứng tỏ rằng hai đoạn thẳng BQ, CN bằng nhau và vuông góc với nhau.
c. Gọi O, O’ là tâm của các hình vuông, I là trung điểm của BC. Chứng minh rằng tam giác OIO’ là tam giác vuông cân.
-
Bài tập 1 trang 201 SBT Hình học 11
Cho hai điểm phân biệt A, B và đường thẳng d song song với đoạn thẳng AB. Điểm C chạy trên đường thẳng d. Tập hợp các trọng tâm của tam giác ABC là
A. một đường thẳng song song với d.
B. hai đường thẳng song song với d.
C. một mặt phẳng song song với d.
D. hai mặt phẳnh song song với d.
-
Bài tập 4 trang 125 SGK Hình học 11 NC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và BD ; P là một điểm thay đổi trên đoạn thẳng AD.
a. Xác định giao điểm Q của mp(MNP) và cạnh AC. Tứ giác MNPQ là hình gì ?
b. Tìm quỹ tích giao điểm I của QM và PN
c. Tìm quỹ tích giao điểm J của QN và PM.
-
Bài tập 5 trang 125 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’. Điểm M nằm giữa A và D, điểm N nằm giữa C và C’ sao cho \(\frac{{AM}}{{MD}} = \frac{{CN}}{{NC'}}\)
a. Chứng minh rằng đường thẳng MN song song với mp(ACB’)
b. Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng đi qua MN và song song với mp(ACB’)
-
Bài tập 6 trang 125 SGK Hình học 11 NC
Cho ba tia Ox, Oy, Oz không đồng phẳng. Chứng minh rằng các tia phân giác ngoài của các góc xOy, yOz và zOx đồng phẳng
-
Bài tập 7 trang 125 SGK Hình học 11 NC
Cho hình chóp S.ABC. Gọi K và N lần lượt là trung điểm của SA và BC ; M là điểm nằm giữa S và C.
a. Chứng minh rằng mặt phẳng đi qua K, song song với AB và SC thì đi qua điểm N.
b. Xác định thiết diện của hình chóp S.ABC khi cắt bởi mp(KMN). Chứng tỏ rằng KN chia thiết diện thành hai phần có diện tích bằng nhau.
-
Bài tập 8 trang 126 SGK Hình học 11 NC
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng \(a\sqrt 2 .\)
a. Tính khoảng cách từ S đến mp(ABCD).
b. Tính khoảng cách giữa đường thẳng AB và mp(SCD)
c. Tính khoảng cách giữa hai đường thẳng AB và SC.
d. Gọi P là mặt phẳng đi qua A và vuông góc với SC. Hãy xác định thiết diện của hình chóp khi cắt bởi (P). Tính diện tích thiết diện.
e. Tính góc giữa đường thẳng AB và mp(P).
-
Bài tập 9 trang 126 SGK Hình học 11 NC
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mp(ABC) và nằm về một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B’, C’ sao cho BB’ = a, CC’ = m.
a. Với giá trị nào của m thì AB’C’ là tam giác vuông ?
b. Khi tam giác AB’C’ vuông tại B’, kẻ AH ⊥ BC. Chứng minh rằng B’C’H là tam giác vuông. Tính góc giữa hai mặt phẳng (ABC) và (AB’C’).
-
Bài tập 2 trang 201 SBT Hình học 11
Cho đường thẳng d có phương trình x + 2y - 4 = 0 trong mặt phẳng Oxy. Đường thẳng d' là ảnh của d qua phép vị tự tâm O, tỉ số -2 có phương trình là
A. x + 2y + 2 = 0 B. - 2x - 4y + 8 = 0
C. x + 2y + 4 = 0 D. x + 2y + 8 = 0
-
Bài tập 3 trang 201 SBT Hình học 11
Cho đường thẳng d có phương trình x + 2y - 4 = 0 trong mặt phẳng Oxy. Đường thẳng d' là đối xứng của đường thẳng d qua trục Oy có phương trình là
A. x + 2y + 2 = 0 B. x - 4y - 8 = 0
C. x - 2y + 4 = 0 D. - x + 2y + 4 = 0
-
Bài tập 4 trang 201 SBT Hình học 11
Tứ diện OABC có các cạnh OA, OB, OC vuông góc với nhau từng đôi một và có OA = a, OB = b, OC = c. Khoảng cách từ điểm O tới mặt phẳng (ABC) là
A. \(\frac{{ac}}{c}\)
B. \(\sqrt {{a^2} + {b^2} + {c^2}} \)
C. \(\frac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
D. \(\frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} \)
-
Bài tập 5 trang 201 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và B. Hình thang có cạnh AD = 2a, AB = BC = a và hình chóp có cạnh SA vuông góc với mặt phẳng (ABCD). Góc \(\widehat {SCD}\) có số đo là
A. 60ο B. 90ο
C. 30ο D. 45ο
-
Bài tập 6 trang 201 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và B. Hình thang có cạnh AD = 2a, AB = BC = a. Hình chóp có cạnh SA = \(a\sqrt 2 \) và SA vuông góc với mặt phẳng (ABCD). Khoảng cách giữa hai đường thẳng AB và SC là
A. \(\frac{{a\sqrt 3 }}{3}\)
B. \(a\sqrt 2 \)
C. \({a\sqrt 6 }\)
D. \(\frac{{a\sqrt 6 }}{3}\)
-
Bài tập 7 trang 202 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a và có mặt bên SAB là tam giác nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD) với \(SA = SB = \frac{{a\sqrt 5 }}{2}\). Khoảng cách giữa hai đường thẳng SC và AB là
A. \(\frac{{a\sqrt 5 }}{2}\)
B. \(\frac{{a\sqrt 2 }}{2}\)
C. \(\frac{{a\sqrt 3 }}{2}\)
D. \(\frac{a}{2}\)
-
Bài tập 8 trang 202 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD). Mặt phẳng (α) qua A và vuông góc với SC cắt SB tại B'. Góc hợp bởi hai đường thẳng AB' và SB có độ lớn là
A. 30ο B. 45ο
C. 60ο D. 90ο
-
Bài tập 9 trang 202 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a. Đường thẳng SO vuông góc mặt phẳng (ABCD) và đoạn SO = \(\frac{a}{2}\). Khoảng cách từ A đến mặt phẳng (SBC) là
A. \(\frac{{a\sqrt 6 }}{4}\)
B. \(\frac{{a\sqrt 3 }}{4}\)
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \({a\sqrt 2 }\)
-
Bài tập 10 trang 202 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và đoạn \(SO = \frac{a}{2}\). Gọi (α) là mặt phẳng qua AD và vuông góc với mặt phẳng (SBC). Góc giữa (α) và (ABCD) có độ lớn là
A. 30ο B. 45ο
C. 60ο D. 90ο
-
Bài tập 11 trang 202 SBT Hình học 11
Cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Khoảng cách từ A đến mặt phẳng (SCD) là
A. \(\frac{{a\sqrt {21} }}{7}\)
B. \(\frac{{a\sqrt 7 }}{{21}}\)
C. \(\frac{{a\sqrt 3 }}{2}\)
D. \(\frac{{a\sqrt 3 }}{6}\)
-
Bài tập 12 trang 202 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, các cạnh bên đều bằng \({a\sqrt 3 }\). Khoảng cách từ S đến mặt phẳng (ABCD) là
A. \(\frac{{a\sqrt 3 }}{4}\)
B. \(\frac{{a\sqrt 3 }}{2}\)
C. \(\frac{{a\sqrt {10} }}{4}\)
D. \(\frac{{a\sqrt {10} }}{2}\)
-
Bài tập 13 trang 203 SBT Hình học 11
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Độ dài đoạn vuông góc chung của A'D' và BC' là
A. \({\frac{a}{2}}\) B. a
C. \({a\sqrt 2 }\) D. \(\frac{{a\sqrt 2 }}{2}\)
-
Bài tập 14 trang 203 SBT Hình học 11
Cho hình vuông ABCD tâm O, cạnh a. Trên hai tia Bx và Dy vuông góc với mặt phẳng (ABCD) và cùng nằm về một phía của mặt phẳng (ABCD) lần lượt lấy hai điểm M và N sao cho: \(BM.DN = \frac{{{a^2}}}{2}\). Đặt \(\widehat {BOM} = \alpha ,\widehat {DON} = \beta \).
Giá trị của biểu thức \(T=\tan \alpha .\tan \beta \) là
A. 1 B. 2
C. 4a2 D. \(\frac{{{a^2}}}{2}\)
-
Bài tập 15 trang 203 SBT Hình học 11
Cho tam giác ABC có A(2;4), B(5;1), C(-1;-2). Phép tịnh tiến \({T_{\overrightarrow {BC} }}\) biến tam giác ABC thành tam giác A'B'C' có tọa độ trọng tâm G' là
A. (4;2) B. (- 4;2)
C. (- 4;-2) D. (4;-2)
-
Bài tập 16 trang 203 SBT Hình học 11
Trong mặt phẳng Oxy, tọa độ ảnh của điểm M(-6;1) qua phép quay Q(O;90ο) là
A. (6;1) B. (1;6)
C. (-6;-1) D. (-1;-6)
-
Bài tập 17 trang 203 SBT Hình học 11
Phương trình ảnh của đường tròn (C): (x - 2)2 + (y + 3)2 = 4 qua phép đối xứng trục Oy là
A. (x + 2)2 + (y - 3)2 = 4
B. (x - 2)2 + (y - 3)2 = 4
C. (x - 2)2 + (y + 3)2 = 4
D. (x + 2)2 + (y + 3)2 = 4
-
Bài tập 18 trang 203 SBT Hình học 11
Ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow u = \left( {3;4} \right)\) là N và ảnh của điểm N qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {1; - 1} \right)\) là P. Độ dài của đoạn thẳng MP là
A. 5 B. \(\sqrt 5 \) C. 4 D. 3
-
Bài tập 19 trang 204 SBT Hình học 11
Cho tứ diện ABCD. Các điểm M, N lần lượt là trung điểm BD, AD. Các điểm H, G lần lượt là trọng tâm các tam giác BCD, ACD. Đường thẳng HG chéo với đường thẳng?
A. MN B. CD C. CN D. AB
-
Bài tập 20 trang 204 SBT Hình học 11
Cho hình chóp S.ABCD, đáy ABCD là hình thang với AD // BC, BC ≤ AD, M là trung điểm SC. Mặt phẳng qua AM và song song với BC cắt đường thẳng SD tại Q. Tỉ số \(\frac{{SQ}}{{SD}}\) có giá trị là
A. \(\frac{4}{3}\) B. \(\frac{3}{4}\) C. \(\frac{1}{2}\) D. 1
-
Bài tập 21 trang 204 SBT Hình học 11
Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi A', B', C', D' lần lượt là trung điểm các cạnh SA, SB, SC, SD. Gọi M là điểm bất kì trên BC. Thiết diện của (A'B'M') với hình chóp S.ABCD là
A. Hình thang B. Hình bình hành
C. Hình thoi D. Hình chữ nhật
-
Bài tập 22 trang 204 SBT Hình học 11
Cho hình chóp S.ABCD với M, N lần lượt là hai điểm lấy trên các cạnh AB, CD. Gọi (α) là mặt phẳng qua MN và song song với SA. Khi đó thiết diện của hình chóp cắt bởi mặt phẳng (α) là
A. hình thang B. hình tam giác
C. hình tứ giác D. hình ngũ giác
-
Bài tập 23 trang 204 SBT Hình học 11
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABC. Hình chiếu song song K của G trên mặt phẳng (BCD) theo phương chiếu AD là
A. trực tâm tam giác BCD.
B. trọng tâm tam giác BCD.
C. một điểm bất kì trong tam giác BCD.
D. điểm H sao cho GH ⊥ (BCD).
-
Bài tập 24 trang 204 SBT Hình học 11
Cho bốn điểm A, B, C, S không cùng nằm trong một mặt phẳng. Gọi I, H lần lượt là trung điểm của SA, AB. Trên SC lấy điểm K sao cho CK = 3KS. Gọi E là giao điểm của đường thẳng BC với mặt phẳng (IHK). Khẳng định nào sau đây là đúng?
A. \(\frac{{BE}}{{BC}} = \frac{1}{3}\)
B. \(\frac{{BE}}{{BC}} = \frac{1}{2}\)
C. \(\frac{{BE}}{{BC}} = \frac{{SK}}{{SC}} = 1\)
D. \(\frac{{BE}}{{BC}} = \frac{{SK}}{{SC}} = \frac{1}{4}\)
-
Bài tập 25 trang 205 SBT Hình học 11
Cho tứ giác ABCD và một điểm S không thuộc mặt phẳng (ABCD). Trên đoạn SC lấy một điểm M không trùng với S và C. Gọi N là giao điểm của đường thẳng SD với mặt phẳng (ABM). Khẳng định nào sau đây là đúng?
A. AN = (ABM) ∩ (SAD) B. AN = (ABM) ∩ (SBC)
C. AN = (ABM) ∩ (SCD) D. AN = (ABM) ∩ (SAC)
-
Bài tập 26 trang 205 SBT Hình học 11
Cho hình hộp ABCD.A'B'C'D' và các điểm M, N lần lượt thuộc các cạnh AB, DD' (M, N không trùng với các đầu mút của các cạnh). Thiết diện của hình hộp bị cắt bởi mặt phẳng (MNB) là
A. hình thoi B. hình chữ nhật
C. hình bình hành D. hình thang cân
-
Bài tập 27 trang 205 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N lần lượt là trung điểm của SD, DC. Điểm P thay đổi trên cạnh BD, BP/BD = k. Để thiết diện của mp(MNP) và hình chóp là tứ giác thì giá trị k thỏa mãn điều kiện nào sau đây?
A. \(0 \le k \le \frac{1}{2}\) B. \(0 \le k \le \frac{2}{3}\)
C. \(\frac{1}{2} \le k \le \frac{3}{4}\) D. \(0 \le k \le \frac{3}{4}\)
-
Bài tập 28 trang 205 SBT Hình học 11
Cho tứ diện ABCD, gọi G1, G2, G3 lần lượt là trọng tâm các tam giác ABC, ACD, ADB. Diện tích thiết diện tạo bởi mặt phẳng (G1G2G3) bằng k lần diện tích tam giác BCD. Giá trị của k là
A. \(\frac{4}{9}\) B. \(\frac{2}{3}\) C. \(\frac{3}{4}\) D. \(\frac{1}{2}\)
-
Bài tập 29 trang 205 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, tam giác SAB đều , SC = SD = \(a\sqrt 3 \). Gọi H, K lần lượt là trung điểm của SA, SB. M là một điểm trên cạnh AD, mặt phẳng (HKM) cắt BC tại N. Đặt AM = x (0 ≤ x ≤ a). Giá trị x để diện tích thiết diện HKMN đạt giá trị nhỏ nhất là
A. x = \(\frac{{3a}}{4}\) B. x = \(\frac{a}{2}\)
C. x = 0 D. x = a.
-
Bài tập 30 trang 205 SBT Hình học 11
Cho hai hình vuông có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF ta lấy các điểm MN sao cho AM = BN. Mặt phẳng (P) chứa MN và song song với AB cắt AD và AF lần lượt tại M', N'. Khẳng định nào sau đây là đúng?
A. MN cắt mp(DFE) B. Tứ giác MNN'M' là hình bình hành
C. AC, BF cắt nhau D. MN song song với mp(DEF)
-
Bài tập 1 trang 125 SGK Hình học 11
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;1),B(0;3),C(2;4). Xác định ảnh của tam giác ABC qua các phép biến hình sau.
(a) Phép tịnh tiến theo vecto \(\vec{v} = (2;1)\).
(b) Phép đối xứng qua trục Ox
(c) Phép đối xứng qua tâm I(2;1).
(d) Phép quay tâm O góc 90o.
(e) Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trụ Oy và phép vị tự tâm O tỉ số k = -2
-
Bài tập 2 trang 125 SGK Hình học 11
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi G và H tương ứng là trọng tâm và trực tâm của tam giác, các điểm A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB.
a) Tìm phép vị tự F biến A, B, C tương ứng thành A’, B’, C’
b) Chứng minh rằng O, G, H thẳng hàng.
c) Tìm ảnh của O qua phép vị tự F.
d) Gọi A”, B”, C” lần lượt là trung điểm của các đoạn thẳng AH, BH, CH; A1, B1, C1 theo thứ tự là giao điểm thứ hai của các tia AH, BH, CH với đường tròn (O); A1’, B1’, C1’ tương ứng là chân các đường cao đi qua A, B, C. Tìm ảnh của A, B, C, A1, B1, C1 qua phép vị tự tâm H tỉ số \(\frac{1}{2}\)
e) Chứng minh chín điểm A’, B’, C’, A”, B”, C”, A1’, B1’, C1’ cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác ABC)
-
Bài tập 3 trang 126 SGK Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.
a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
c) Lấy một điểm K trên đoạn SE và gọi C' = SC ∩ KB, D'= SD ∩ KA. Chứng minh rằng hai giao điểm của AC' và BD' thuộc đường thẳng d nói trên.
-
Bài tập 1 trang 199 SBT Hình học 11
Cho hình chóp tứ giác đều S.ABCD. Gọi H là chân đường cao của hình chóp. Một mặt phẳng (P) thay đổi cắt các cạnh bên SA, SB, SC, SD lần lượt tại E, F, I, J. Gọi K = EI ∩ FJ. Đặt SE = a, SF = b, SI = c, SJ = d, SK = k, ∠ASH = α.
a) Tìm diện tích của tam giác SEI theo a, c, \(\alpha\).
b) Chứng minh rằng \(\frac{1}{a} + \frac{1}{b} = \frac{{2\cos \alpha }}{k}\)
Suy ra \(\frac{1}{a} + \frac{1}{c} = \frac{1}{b} + \frac{1}{d}\)
-
Bài tập 4 trang 126 SGK Hình học 11
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có E, F, M và N lần lượt là trung điểm của AC, BD, AC’ và BD’. Chứng minh MN = EF.
-
Bài tập 5 trang 126 SGK Hình học 11
Cho hình lập phương ABCD.A'B'C'D' có E và F lần lượt là trung điểm của các cạnh AB và DD'. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC') và (EFK) với K là trung điểm của cạnh B'C'.
-
Bài tập 2 trang 199 SBT Hình học 11
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
-
Bài tập 6 trang 126 SGK Hình học 11
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD' và B'C.
b)Tính khoảng cách của hai đường thẳng BD' và B'C.
-
Bài tập 7 trang 126 SGK Hình học 11
Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C', D' lần lượt là hình chiếu vuông góc của A trên SC và SD . Chứng minh rằng :
a) \(\widehat{SBC}=\widehat{SCD}=90^0\)
b) AD’,AC’ và AB cùng nằm trên một mặt phẳng.
c) Chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định kho S di động trên tia Ax.
-
Bài tập 3 trang 199 SBT Hình học 11
Cho tứ diện SABC có SA, SB, SC vuông góc với nhau từng đôi một. Gọi H là hình chiếu vuông góc của S lên mp(ABC).
a) Chứng minh rằng H là trực tâm của tam giác ABC.
b) Chứng minh rằng \(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}}\)
c) Chứng minh rằng (SSBC)2 = (SHBC). (SABC) và (SABC)2 = (SSAB)2 + (SSBC)2 + (SSCA)2
d) Chứng minh rằng \(S{G^2} = \frac{{S{A^2} + S{B^2} + S{C^2}}}{9}\) (G là trọng tâm của tam giác ABC) và (AB + BC + CA)2 ≤ 6(SA2 + SB2 + SC2).
e) Chứng minh rằng tam giác ABC có ba góc nhọn và SA2tanA = SB2tanB = SC2tanC = 2SABC
-
Bài tập 4 trang 200 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên đáy ABCD trùng với trọng tâm tam giác ABD. Mặt bên (SAB) tạo với đáy góc 60ο. Tính theo a khoảng cách từ B đến mặt phẳng (SAD)


