Bài tập 7 trang 126 SGK Hình học 11

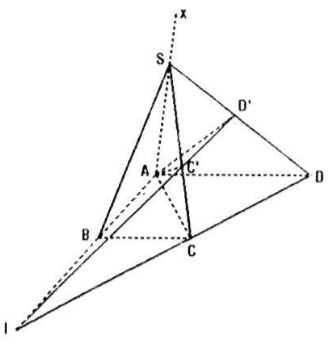
Câu a:

Dễ thấy \(AD\perp (SAB)\) và do BC // AD.

\(\Rightarrow BC\perp (SAD)\Rightarrow BC\perp SB\Rightarrow \widehat{SBC}=90^0\)

* Ta tính được \(CD=CA=a\sqrt{2}\) mà \(AD = 2a \Rightarrow \Delta ACD\) vuông tại C

\(\Rightarrow CD\perp AC\)

Mặt khác \(SA\perp (ABCD)\Rightarrow CD\perp SA\)

\(\Rightarrow CD\perp (SAC)\Rightarrow CD\perp SC\)

\(\Rightarrow \widehat{SCD}=90^0\)

Câu b:

Theo chứng minh câu a) \(CD\perp (SAC), AC'\subset (SAC)\Rightarrow CD\perp AC'\)

Hơn nữa \(AC'\perp SC\) suy ra:

\(AC'\perp (SCD)\Rightarrow AC'\perp SD\)

Dễ thấy \(AB\perp (SCD)\Rightarrow AB\perp SC\)

Suy ra AC', AD', AB cùng vuông góc với SC ⇒ AC', AD', AB cùng nằm trên mặt phẳng vuông góc với SC hay AC', AD', AB cùng nằm trên một mặt phẳng.

Câu c:

 Theo chứng minh câu b) AC', AD', AB cùng nằm trên một mặt phẳng, gọi đó là mặt phẳng \((\alpha )\)

Gọi I là giao điểm của AB và CD ⇒ ID' là giao tuyến của mặt phẳng (SCD) và \((\alpha )\)

Dễ thấy C' \(\in\) SC; C' \(\in\) AC' ⇒ C' nằm trên giao tuyến của \((\alpha )\) và (SCD) ⇒ C', D', I thẳng hàng hay C'D' luôn đi qua I khi S thay đổi trên Ax. (đpcm)

-- Mod Toán 11 HỌC247