Giải bài 4 tr 200 SBT Hình học 11
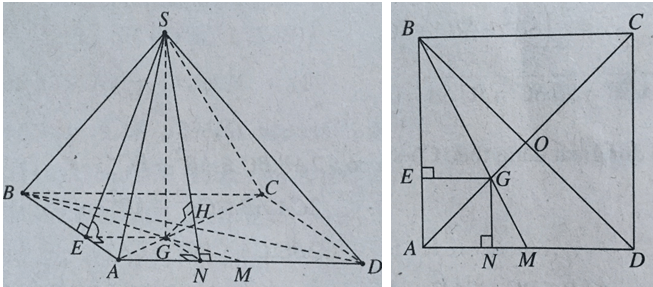
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên đáy ABCD trùng với trọng tâm tam giác ABD. Mặt bên (SAB) tạo với đáy góc 60ο. Tính theo a khoảng cách từ B đến mặt phẳng (SAD)
Hướng dẫn giải chi tiết
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
\(\left\{ \begin{array}{l}
AB \bot SG\\
AB \bot GE
\end{array} \right. \Rightarrow AB \bot \left( {SEG} \right) \Rightarrow AB \bot SE\)
\(\left\{ \begin{array}{l}
SE \bot AB\\
GE \bot AB
\end{array} \right. \Rightarrow \left( {\widehat {\left( {SAB} \right),\left( {ABCD} \right)}} \right) = \widehat {SEG} = {60^0}\)
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ⊥ AD. Tương tự như trên, ta có: \(\left\{ \begin{array}{l}
AD \bot GN\\
AD \bot SG
\end{array} \right. \Rightarrow AD \bot \left( {SGN} \right)\)
Hạ GH ⊥ SN, ta có GH ⊥ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
Trong tam giác vuông SGN, ta có: \(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}}\,\,\left( 1 \right)\)
Do GN // AB nên \(\frac{{GN}}{{BA}} = \frac{{MG}}{{MB}} = \frac{1}{3}\). Ta có: \(GN = \frac{{BA}}{3} = \frac{a}{3}\)
Trong tam giác SGE, ta được \(GS = GE.\tan {60^0} = \frac{{a\sqrt 3 }}{3}\) (do GE = GN). Thế vào (1) ta được:
\(\frac{1}{{G{H^2}}} = \frac{1}{{{{\left( {\frac{a}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} = \frac{1}{{{{\left( {\frac{a}{3}} \right)}^2}}}.\frac{4}{3} \Rightarrow GH = \frac{{a\sqrt 3 }}{6}\)
Ta có: M ∈ (SAD) và MB = 3MG ⇒ d(B,(SAD)) = 3d(G,(SAD)) = \(\frac{{a\sqrt 3 }}{2}\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 5 trang 200 SBT Hình học 11
Bài tập 6 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 30 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 2 trang 199 SBT Hình học 11
Bài tập 6 trang 126 SGK Hình học 11
-


Hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\). Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) có số đo là đáp án?
bởi Trinh Hung
 17/07/2021
17/07/2021
A. \({30^0}\) B. \({45^0}\)
C. \({135^0}\) D. \({60^0}\)
Theo dõi (0) 1 Trả lời -


Với hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\). Biết rằng \(SA = SB = SC = SD\). Chọn khẳng định sai?
bởi Phung Meo
 17/07/2021
17/07/2021
A. \(AB//\left( {SCD} \right)\) B. \(AC \bot \left( {SBD} \right)\)
C. \(SO \bot \left( {ABCD} \right)\) D. \(AD \bot \left( {SAB} \right)\)
Theo dõi (0) 1 Trả lời -


Ta cho tứ diện \(ABCD\) có \(M\) là trung điểm \(AB,\,\,N\) là trung điểm \(AC\). Mệnh đề nào sau đây đúng?
bởi Nguyen Ngoc
 17/07/2021
17/07/2021
A. Ba vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} \) đồng phẳng
B. Ba vectơ \(\overrightarrow {BA} ,\,\,\overrightarrow {CB} ,\,\,\overrightarrow {BD} \) đồng phẳng
C. Ba vectơ \(\overrightarrow {BD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} \) đồng phẳng
D. Ba vectơ \(\overrightarrow {AD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} \) đồng phẳng
Theo dõi (0) 1 Trả lời