Giải bài 30 tr 205 SBT Hình học 11
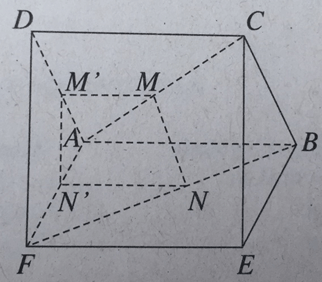
Cho hai hình vuông có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF ta lấy các điểm MN sao cho AM = BN. Mặt phẳng (P) chứa MN và song song với AB cắt AD và AF lần lượt tại M', N'. Khẳng định nào sau đây là đúng?
A. MN cắt mp(DFE) B. Tứ giác MNN'M' là hình bình hành
C. AC, BF cắt nhau D. MN song song với mp(DEF)
Hướng dẫn giải chi tiết
Ta có: \(\left\{ \begin{array}{l}
\left( P \right)\parallel AB\\
\left( P \right) \cap \left( {ABCD} \right) = MM'
\end{array} \right. \Rightarrow MM'\parallel AB \Rightarrow MM' \bot EF\,\,\left( 1 \right)\)
Tương tự NN’ // EF ⇒ MM’ // NN’. Từ đó ta vẽ được các điểm M’, N’ như hình vẽ và quan sát thấy MNN’M’ mới là hình thang chưa thể là hình bình hành.
Dễ dàng quan sát thấy M’N’ // DF hoặc chứng minh được khẳng định đó như sau:
\[\begin{array}{l}
MN'\parallel CD \Rightarrow \frac{{AM'}}{{AD}} = \frac{{AM}}{{AC}}\\
NN'\parallel AB \Rightarrow \frac{{AN'}}{{AF}} = \frac{{BN}}{{BF}}
\end{array}\)
Mà \(AC = BF,AM = BN \Rightarrow \frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)
\( \Rightarrow \frac{{AM'}}{{AD}} = \frac{{AN'}}{{AF}} \Rightarrow M'N'\parallel DF\,\,\left( 2 \right)\)
Từ (1), (2) ⇒ (MNN’M’) // (DEF) ⇒ MN // (DEF)
Đáp án: D
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 5 trang 200 SBT Hình học 11
Bài tập 6 trang 200 SBT Hình học 11
Bài tập 7 trang 200 SBT Hình học 11
Bài tập 8 trang 200 SBT Hình học 11
Bài tập 9 trang 200 SBT Hình học 11
Bài tập 1 trang 124 SGK Hình học 11 NC
Bài tập 2 trang 124 SGK Hình học 11 NC
Bài tập 3 trang 125 SGK Hình học 11 NC
Bài tập 1 trang 201 SBT Hình học 11
Bài tập 4 trang 125 SGK Hình học 11 NC
Bài tập 5 trang 125 SGK Hình học 11 NC
Bài tập 6 trang 125 SGK Hình học 11 NC
Bài tập 7 trang 125 SGK Hình học 11 NC
Bài tập 8 trang 126 SGK Hình học 11 NC
Bài tập 9 trang 126 SGK Hình học 11 NC
Bài tập 2 trang 201 SBT Hình học 11
Bài tập 3 trang 201 SBT Hình học 11
Bài tập 4 trang 201 SBT Hình học 11
Bài tập 5 trang 201 SBT Hình học 11
Bài tập 6 trang 201 SBT Hình học 11
Bài tập 7 trang 202 SBT Hình học 11
Bài tập 8 trang 202 SBT Hình học 11
Bài tập 9 trang 202 SBT Hình học 11
Bài tập 10 trang 202 SBT Hình học 11
Bài tập 11 trang 202 SBT Hình học 11
Bài tập 12 trang 202 SBT Hình học 11
Bài tập 13 trang 203 SBT Hình học 11
Bài tập 14 trang 203 SBT Hình học 11
Bài tập 15 trang 203 SBT Hình học 11
Bài tập 16 trang 203 SBT Hình học 11
Bài tập 17 trang 203 SBT Hình học 11
Bài tập 18 trang 203 SBT Hình học 11
Bài tập 19 trang 204 SBT Hình học 11
Bài tập 20 trang 204 SBT Hình học 11
Bài tập 21 trang 204 SBT Hình học 11
Bài tập 22 trang 204 SBT Hình học 11
Bài tập 23 trang 204 SBT Hình học 11
Bài tập 24 trang 204 SBT Hình học 11
Bài tập 25 trang 205 SBT Hình học 11
Bài tập 26 trang 205 SBT Hình học 11
Bài tập 27 trang 205 SBT Hình học 11
Bài tập 28 trang 205 SBT Hình học 11
Bài tập 29 trang 205 SBT Hình học 11
Bài tập 1 trang 125 SGK Hình học 11
Bài tập 2 trang 125 SGK Hình học 11
Bài tập 3 trang 126 SGK Hình học 11
Bài tập 1 trang 199 SBT Hình học 11
Bài tập 4 trang 126 SGK Hình học 11
Bài tập 5 trang 126 SGK Hình học 11
Bài tập 2 trang 199 SBT Hình học 11
Bài tập 6 trang 126 SGK Hình học 11
Bài tập 7 trang 126 SGK Hình học 11
-


Cho tứ diện \(ABCD\) có \(AC = 6a\) và có \(BD = 8a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AD,\,\,BC\). Biết \(AC \bot BD\). Tính độ dài đoạn thẳng \(MN\).
bởi Naru to
 18/07/2021
18/07/2021
A. \(MN = a\sqrt {10} \) B. \(MN = 7a\)
C. \(MN = 5a\) D. \(MN = 10a\)
Theo dõi (0) 1 Trả lời -


Cho biêt tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(M\) là trung điểm của \(BC\). Tính cosin của góc giữa hai đường thẳng \(AB\) và \(DM\).
bởi An Vũ
 18/07/2021
18/07/2021
A. \(\dfrac{{\sqrt 3 }}{6}\) B. \(\dfrac{1}{2}\)
C. \(\dfrac{{\sqrt 3 }}{2}\) D. \(\dfrac{{\sqrt 2 }}{2}\)
Theo dõi (0) 1 Trả lời -


Cho hình chóp là \(S.ABC\) có \(SA = SB = SC.\) Gọi \(I\) là hình chiếu vuông góc của \(S\) lên mặt phằng \(\left( {ABC} \right)\). Chọn khẳng định đúng trong các khẳng định sau.
bởi Mai Hoa
 17/07/2021
17/07/2021
A. \(I\) là trực tậm của \(\Delta ABC\)
B. \(I\) là trung điểm của \(AB\)
C. \(I\)là tâm đường tròn ngoại tiếp của \(\Delta ABC\)
D. \(I\) là trọng tâm của \(\Delta ABC\)
Theo dõi (0) 1 Trả lời