Giải bài 3.11 tr 139 SBT Hình học 11
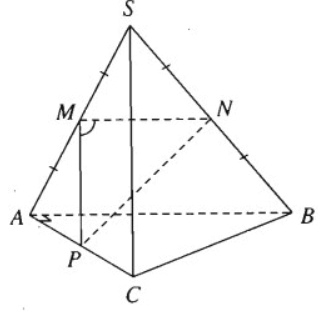
Cho hình chóp A.ABC có SA = SB = SC = AB = AC = a và \(BC = a\sqrt 2 \). Tính góc giữa hai đường thẳng AB và SC.
Hướng dẫn giải chi tiết
Gọi M, N, P lần lượt là trung điểm của SA, SB. AC. Để tính góc giữa hai đường thẳng SC và AB, ta cần tính ∠NMP.
Ta có:
\(\begin{array}{l}
NB = MP = \frac{a}{2},S{P^2} = \frac{{3{a^2}}}{4},B{P^2} = \frac{{5{a^2}}}{4}\\
P{B^2} + S{P^2} = 2N{P^2} + \frac{{S{B^2}}}{2} \Rightarrow N{P^2} = \frac{{3{a^2}}}{4}
\end{array}\)
Mặt khác:
\(\begin{array}{l}
N{P^2} = N{M^2} + M{P^2} - 2MN.MP.\cos \widehat {NMP}\\
\Rightarrow \cos \widehat {NMP} = - \frac{{\frac{{{a^2}}}{4}}}{{2.\frac{a}{2}.\frac{a}{2}}} = - \frac{1}{2} \Rightarrow \widehat {NMP} = {120^0}
\end{array}\)
Vậy góc giữa hai đường thẳng SC và AB bằng 60ο.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.9 trang 138 SBT Hình học 11
Bài tập 3.10 trang 138 SBT Hình học 11
Bài tập 3.12 trang 139 SBT Hình học 11
Bài tập 3.13 trang 139 SBT Hình học 11
Bài tập 3.14 trang 139 SBT Hình học 11
Bài tập 3.15 trang 139 SBT Hình học 11
Bài tập 7 trang 95 SGK Hình học 11 NC
Bài tập 8 trang 95 SGK Hình học 11 NC
Bài tập 9 trang 96 SGK Hình học 11 NC
-


Cho hình chop S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA=(a√6)/3. Tính góc giữa SC với (ABCD)
bởi Hiền Chít
 24/03/2020
Giải giúp e câu 18 19 20
24/03/2020
Giải giúp e câu 18 19 20 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình chop S.ABCD có đáy ABCD là hình vuông, SA vuông góc với (ABCD). Gọi M, N lần lượt là trung điểm của SB, SC. Chứng minh: BD vuông góc (SAC), MN vuông góc (SAB)
bởi Kỳ Khương Nhật
 23/03/2020
Bài tập trong hình
23/03/2020
Bài tập trong hình Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tam giác SAD là tam giác gì biết hình chóp S.ABCD với ABCD là hình vuông cạnh a?
bởi Nguyễn Thị Kim Khôi
 23/02/2020
23/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Cho hình chóp SABC có SA=SB và CA=CB. Chứng minh rằng SC vuông góc ABTheo dõi (0) 2 Trả lời
Cho hình chóp SABC có SA=SB và CA=CB. Chứng minh rằng SC vuông góc ABTheo dõi (0) 2 Trả lời