Giải bài 2.30 tr 78 SBT Hình học 11
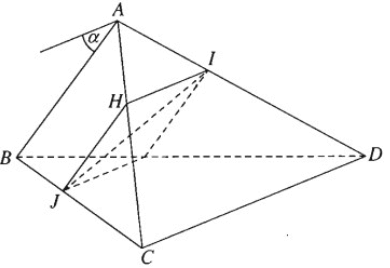
Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho \(\frac{{IA}}{{ID}} = \frac{{JB}}{{JC}}\). Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định.
Hướng dẫn giải chi tiết
Qua I kẻ đường thẳng song song với CD cắt AC tại H, ta có \(\frac{{HA}}{{HC}} = \frac{{IA}}{{ID}}\)
Mặt khác: \(\frac{{IA}}{{ID}} = \frac{{JB}}{{JC}}\)
Suy ra : HJ // AB
Như vậy mặt phẳng (IJH) song song với AB và CD.
Gọi (α) là mặt phẳng qua AB và song song với CD, ta có
\(\left\{ \begin{array}{l}
\left( \alpha \right)\parallel \left( {IJH} \right)\\
IJ \subset \left( {IJH} \right)
\end{array} \right. \Rightarrow IJ\parallel \left( \alpha \right)\)
Vậy IJ song song với mặt phẳng (α) cố định.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 2.28 trang 77 SBT Hình học 11
Bài tập 2.29 trang 77 SBT Hình học 11
Bài tập 2.31 trang 78 SBT Hình học 11
Bài tập 29 trang 67 SGK Hình học 11 NC
Bài tập 30 trang 67 SGK Hình học 11 NC
Bài tập 31 trang 68 SGK Hình học 11 NC
Bài tập 32 trang 68 SGK Hình học 11 NC
Bài tập 33 trang 68 SGK Hình học 11 NC
Bài tập 34 trang 68 SGK Hình học 11 NC
Bài tập 35 trang 68 SGK Hình học 11 NC
Bài tập 36 trang 68 SGK Hình học 11 NC
Bài tập 37 trang 68 SGK Hình học 11 NC
-


Xác định giao tuyến Q của đường thẳng BB' và (MNP) biết M, N là trung điểm của AA', CC'
bởi Trần Sáng
 30/12/2019
30/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hình hộp abcd.a'b'c'd', gọi m,n lần lượt là trung điểm của 2 cạnh aa' và cc'?
bởi Trần Sáng
 30/12/2019
Bài 17
30/12/2019
Bài 17 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời