Bài 1 trang 113 SGK Toán 11 Cánh diều Tập 1
Cho hình hộp \(ABCD.A’B’C D’\).
a) Chứng minh rằng \((ACB’) // (A’C’D)\)?
b) Gọi G1, G2 lần lượt là giao điểm của BD’ với các mặt phẳng \((ACB’)\) và \((A’C’D)\). Chứng minh rằng G1, G2 lần lượt là trọng tâm của hai tam giác \(ACB’\) và \(A’C’D\)?
c) Chứng minh rằng BG1 = G1G2 = D’G2?
Hướng dẫn giải chi tiết Bài 1
a)
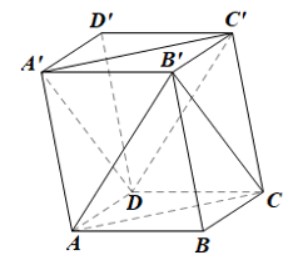
Ta có: (ABCD) // (A’B’C’D’) ( do ABCD.A’B’C’D’ là hình hộp);
(ABCD) ∩ (ACC’A’) = AC;
(A’B’C’D’) ∩ (ACC’A’) = A’C’.
Do đó AC // A’C’.
Mà A’C’ ⊂ (A’C’D) nên AC // (A’C’D).
Chứng minh tương tự ta cũng có AB’ // DC’ mà DC’ ⊂ (A’C’D) nên AB’ // (A’C’D).
Ta có: AC // (A’C’D);
AB’ // (A’C’D);
AC, AB’ cắt nhau tại điểm A và cùng nằm trong mp(ACB’).
Do đó (ACB’) // (A’C’D).
b)

- Gọi O là tâm hình bình hành đáy ABCD, I là giao điểm của BD’ và DB’.
Tứ giác BDD’B’ có BB’ // DD’ và BB’ = DD’ nên là hình bình hành.
Do đó hai đường chéo BD’ và DB’ cắt nhau tại trung điểm I của mỗi đường.
Trong mp(BDD’B’), BD’ cắt B’O tại G1.
Mà B’O ⊂ (ACB’) nên G1 là giao điểm của BD’ với (ACB’).
Trong mp(BDD’B’), xét BDB’ có hai đường trung tuyến BI, B’O cắt nhau tại G1 nên G1 là trọng tâm của DBDB’
Do đó
Trong (ACB’), xét ACB’ có B’O là đường trung tuyến và
Suy ra G1 là trọng tâm của ACB’.
- Gọi O’ là tâm hình bình hành đáy A’B’C’D’.
Chứng minh tương tự như trên ta cũng có: G2 là trọng tâm của DD’B’ nên
Trong (A’C’D), A’C’D có DO’ là đường trung tuyến và
Suy ra G2 là trọng tâm của A’C’D.
c) Theo chứng minh câu b, ta có:
- G1 là trọng tâm của BDB’ nên và
- G2 là trọng tâm của DD’B’ nên và
Do đó và
Ta có: và BI = D’I (do I là trung điểm của BD’)
Suy ra BG1 = D’G2.
Lại có nên IG1 = IG2 = BG1
Do đó G1G2 = IG1 + IG2 = BG1 + BG1 = BG1.
Vậy BG1 = G1G2 = D’G2.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Hoạt động 4 trang 112 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 3 trang 113 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 2 trang 113 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 3 trang 113 SGK Toán 11 Cánh diều Tập 1 - CD
Bài tập 36 trang 112 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 37 trang 112 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 38 trang 112 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 39 trang 113 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 40 trang 113 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 41 trang 113 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 42 trang 113 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 43 trang 113 SBT Toán 11 Tập 1 Cánh diều - CD
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


