Bài 2 trang 88 SGK Toán 11 Tập 2 Cánh diều - CD

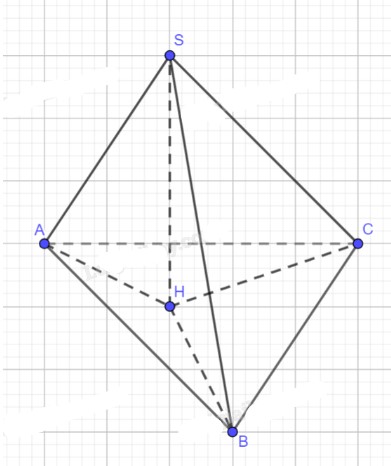
a)

- H là hình chiếu của S trên mặt phẳng (ABC)

- A là hình chiếu của A trên mặt phẳng (ABC)

\( \Rightarrow \) HA là hình chiếu của SA trên mặt phẳng (ABC)

- H là hình chiếu của S trên mặt phẳng (ABC)

- B là hình chiếu của B trên mặt phẳng (ABC)

\( \Rightarrow \) HB là hình chiếu của SB trên mặt phẳng (ABC)

- H là hình chiếu của S trên mặt phẳng (ABC)

- C là hình chiếu của C trên mặt phẳng (ABC)

\( \Rightarrow \) HC là hình chiếu của SC trên mặt phẳng (ABC)

b) Do H là hình chiếu của S trên mặt phẳng (ABC) \( \Rightarrow SH \bot (ABC)\).

Mà \(AB,AC,BC \subset (ABC) \Rightarrow SH \bot AB,SH \bot AC,SH \bot BC\).

Ta có: \(\left\{ \begin{array}{l}SA \bot BC\\SH \bot BC\\SA \cap SH = S\\SA,SH \subset (SAH)\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,(1)\)

Tương tự \(\left\{ \begin{array}{l}SC \bot AB\\SH \bot AB\\SC \cap SH = S\\SC,SH \subset (SCH)\end{array} \right. \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,(2)\)

TỪ (1) và (2) \( \Rightarrow \) H là trực tâm của tam giác ABC.

Vì \(\left\{ \begin{array}{l}AB \bot (SCH)\\SC \subset (SCH)\end{array} \right. \Rightarrow AB \bot SC\)

-- Mod Toán 11 HỌC247