Bài tập 21 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

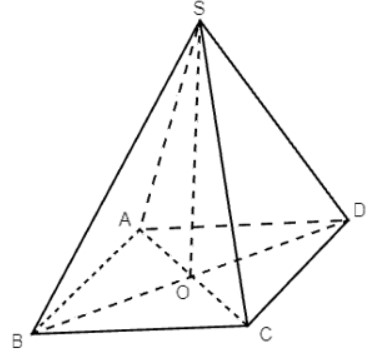
Gọi O là hình chiếu của S trên (ABCD). Khi đó SO ⊥ (ABCD).

Mà OA, OB, OC, OD đều nằm trên (ABCD) nên SO ⊥ OA, SO ⊥ OB, SO ⊥ OC, SO ⊥ OD.

Xét tam giác SOA và tam giác SOB có:

$\widehat{SOA}=\widehat{SOB}=90°;$

SA = SB (gt);

SO chung

Suy ra ∆SOA = ∆SOB (cạnh huyền – cạnh góc vuông)

Do đó: OA = OB (hai cạnh tương ứng)

Tương tự: ∆SOB = ∆SOC = ∆SOD nên OB = OC = OD.

Từ đó ta có: OA = OB = OC = OD hay O là tâm đường tròn đi qua bốn đỉnh của tứ giác ABCD.

-- Mod Toán 11 HỌC247