Bài tập 23 trang 95 SBT Toán 11 Tập 2 Cánh diều
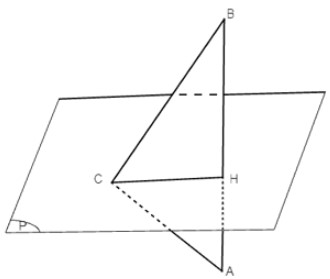
Cho đoạn thẳng AB và mặt phẳng (P) sao cho (P) ⊥ AB và (P) cắt đoạn thẳng AB tại điểm H thoả mãn HA = 4 cm, HB = 9 cm. Điểm C chuyển động trong mặt phẳng (P) thoả mãn \(\widehat{ACB}={{90}^{0}}\). Chứng minh rằng điểm C thuộc đường tròn tâm H bán kính 6 cm trong mặt phẳng (P)?
Hướng dẫn giải chi tiết Bài tập 23
Vì nên A, B, C không thẳng hàng.
Ta có: AB ⊥ (P), HC ⊂ (P) nên AB ⊥ HC.
Áp dụng hệ thức lượng trong tam giác ACB vuông tại C ta có:
HC2 = HA.HB = 4.9 = 36, suy ra HC = 6 (cm).
Ta thấy khi C chuyển động trong mặt phẳng (P) thoả mãn thì C luôn cách H (với H là điểm cố định) một khoảng không đổi HC = 6 cm.
Vậy C thuộc đường tròn tâm H bán kính 6 cm trong (P).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.



