Bài tập 15 trang 95 SBT Toán 11 Tập 2 Cánh diều - CD

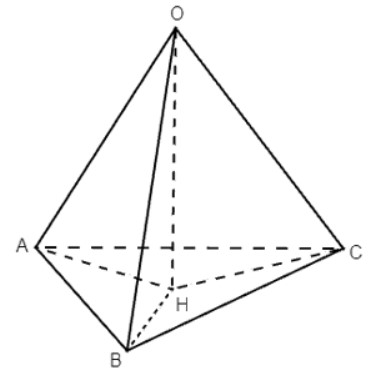
Vì $\widehat{OHA}=\widehat{OHB}=90°$ nên ta có OH ⊥ HA, OH ⊥ HB mà HA và HB cắt nhau tại H trong (HAB) nên OH ⊥ (HAB).

Vì $\widehat{OHB}=\widehat{OHC}=90°$ nên ta có OH ⊥ HB, OH ⊥ HC mà HB và HC cắt nhau tại H trong (HBC) nên OH ⊥ (HBC).

Ta thấy: (HAB) và (HBC) cùng đi qua H và vuông góc với OH nên (HAB) ≡ (HBC).

Hay (HAB) ≡ (HBC) ≡ (ABC).

Suy ra: H thuộc mặt phẳng (ABC).

-- Mod Toán 11 HỌC247