Hoạt động khám phá 1 trang 61 SGK Toán 10 Chân trời sáng tạo tập 1
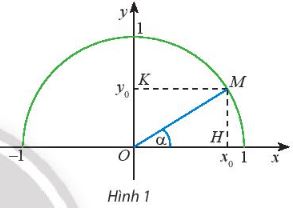
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
Hướng dẫn giải chi tiết Hoạt động khám phá 1
Phương pháp giải
Tam giác vuông OHM có \(\alpha = \widehat {xOM}\)
\(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}};\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\)
Lời giải chi tiết
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}}.\)
Mà \(MH = {y_0};OH = {x_0};OM = 1.\)
\( \Rightarrow \sin \alpha = \frac{{{y_0}}}{1} = {y_0};\;\cos \alpha = \frac{{{x_0}}}{1} = {x_0}\;.\)
\( \Rightarrow \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}.\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Thực hành 1 trang 62 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 62 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 63 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 64 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 65 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 69 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


a) Phân tích I theo AB và AC.
b) Chứng minh I đi qua G của tam giác ABC.
c) I cắt BC tại M. Chứng tỏ hệ thức 3MB+MC=0. Tính tỉ số MI/MJ
Theo dõi (0) 0 Trả lời