Giải bài 6.32 trang 21 SBT Toán 10 Kết nối tri thức tập 2
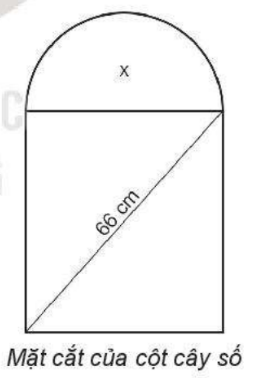
Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật (xem hình bên). Biết rằng đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 66 cm. Tìm kích thước của hình chữ nhật, biết rằng diện tích của phần nửa hình tròn bằng 0,3 lần diện tích của phần hình chữ nhật. Lấy \(\pi = 3,14\) và làm tròn kết quả đến chữ số thập phân thứ hai.
Hướng dẫn giải chi tiết Bài 6.32
Phương pháp giải
Bước 1: Gọi x là đường kính của nửa hình tròn, biểu diễn diện tích S1 của nửa hình tròn và diện tích S2 của hình chữ nhật theo x
Bước 2: Sử dụng giả thiết S1 = 0,3S2, ta thu được PT bậc hai của x
Bước 3: Giải PT vừa tìm được, suy ra điều kiện của x. Kết luận.
Lời giải chi tiết
Gọi x (cm) (0 < x < 66) là đường kính của nửa hình tròn
\( \Rightarrow \) Kích thước còn lại của hình chữ nhật là y = \(\sqrt {{{66}^2} - {x^2}} = \sqrt {4356 - {x^2}} \) (cm)
DIện tích của nửa hình tròn là: \({S_1} = \frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} = \frac{{3,14}}{8}{x^2}\) (cm2)
Diện tích hình chữ nhật là: \({S_2} = x\sqrt {4356 - {x^2}} \) (cm2)
Theo giả thiết, \({S_1} = 0,3{S_2} \Leftrightarrow \frac{{3,14}}{8}{x^2} = 0,3.x\sqrt {4356 - {x^2}} \)
\( \Leftrightarrow \frac{{3,14}}{8}{x^2} - 0,3.x\sqrt {4356 - {x^2}} = 0 \Leftrightarrow x\left( {\frac{{3,14}}{8}x - 0,3\sqrt {4356 - {x^2}} } \right)\) = 0
\( \Leftrightarrow \frac{{3,14}}{8}x - 0,3\sqrt {4356 - {x^2}} = 0\) (do x > 0) \( \Leftrightarrow \sqrt {4356 - {x^2}} = \frac{{157}}{{120}}x\) (*)
Bình phương hai vế của (*) ta được: \(4356 - {x^2} = \frac{{24649}}{{14400}}{x^2} \Leftrightarrow {x^2} \approx 1606,35 \Leftrightarrow x \approx 40,08\)
Với x = 40,08 thì y = 52,44
Vậy hai kích thước của hình chữ nhật là 40,08 cm và 52,44 cm
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


