Giải bài 5 trang 19 SBT Toán 10 Chân trời sáng tạo tập 2
Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc \(60^\circ \) đến vị trí A sau đó đi tiếp 3 m đến vị trí B như hình 1.
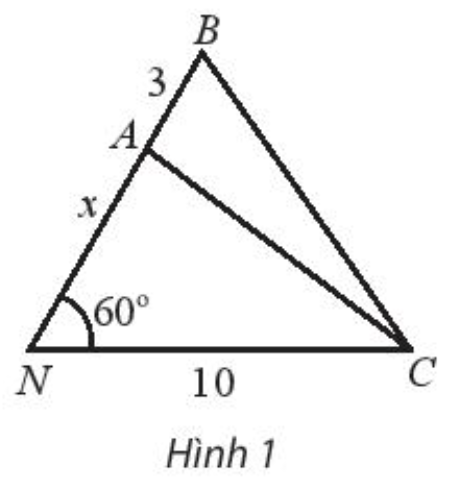
a) Biểu diễn khoảng cách AC và BC theo x
b) Tìm x để \(AC = \frac{8}{9}BC\)
c) Tìm x để khoảng cách \(BC = 2AN\)
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
a) Sử dụng định lí côsin \(a = \sqrt {{b^2} + {c^2} - 2bc\cos A} \)
b) Lập phương trình dựa vào kết quả của câu a) và giải phương trình
c) Lập phương liên quan và giải phương trình
Lời giải chi tiết
a) Áp dụng đính lí côsin trong tam giác ANC ta có:
\(\begin{array}{l}AC = \sqrt {A{N^2} + N{C^2} - 2AN.NC.\cos \widehat N} = \sqrt {{x^2} + {{10}^2} - 2x.10.\cos 60^\circ } \\ = \sqrt {{x^2} - 10x + 100} \end{array}\)
Áp dụng đính lí côsin trong tam giác BNC ta có:
\(\begin{array}{l}BC = \sqrt {B{N^2} + N{C^2} - 2BN.NC.\cos \widehat N} = \sqrt {{{\left( {x + 3} \right)}^2} + {{10}^2} - 2\left( {x + 3} \right).10.\cos 60^\circ } \\ = \sqrt {{x^2} - 4x + 79} \end{array}\)
b) Ta có: \(AC = \frac{8}{9}BC\) hay
\(\begin{array}{l}\sqrt {{x^2} - 10x + 100} = \frac{8}{9}\sqrt {{x^2} - 4x + 79} \\ \Rightarrow {x^2} - 10x + 100 = \frac{{64}}{{81}}\left( {{x^2} - 4x + 79} \right)\\ \Rightarrow \frac{{17}}{{81}}{x^2} - \frac{{554}}{{81}}x + \frac{{3044}}{{81}} = 0\end{array}\)
\( \Rightarrow x \simeq 7\) hoặc \(x \simeq 25,6\)
Thay hai giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn
Vậy khi \(x \simeq 7\) hoặc \(x \simeq 25,6\) thì \(AC = \frac{8}{9}BC\)
c) Yêu cầu bài toán tương đương
\(\begin{array}{l}\sqrt {{x^2} - 4x + 79} = 2x\\ \Rightarrow {x^2} - 4x + 79 = 4{x^2}\\ \Rightarrow 3{x^2} + 4x - 79 = 0\end{array}\)
\( \Rightarrow x = \frac{{ - 2 - \sqrt {241} }}{3}\) hoặc \(x = \frac{{ - 2 + \sqrt {241} }}{3}\)
Mà vì \(x \ge 0\) nên \(x = \frac{{ - 2 + \sqrt {241} }}{3}\)
Vậy khi \(x = \frac{{ - 2 + \sqrt {241} }}{3}\) thì \(BC = 2AN\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





