Bài tập 6.13 trang 181 SBT Toán 10

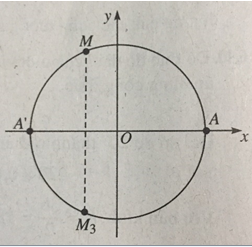
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, \(\frac{\pi }{2}\) < α < π, A(1; 0). Gọi M₃ là điểm đối xứng với M qua trục Ox. Số đo của cung AM3 là

A. π - α + k2π, k ∈ Z          B. α +\(\frac{\pi }{2}\) + k2π, k ∈ Z

C. α - π + k2π, k ∈ Z          D. - α + k2π, k ∈ Z