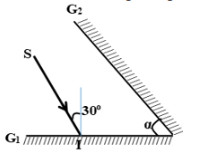
Hai gương phẳng G1 và G2 có mặt phản xạ quay vào nhau và tạo với nhau một góc α (hình vẽ). Tia tới SI được chiếu lên gương G1 lần lượt phản xạ một lần trên gương G1 rồi một lần trên gương G2. Biết góc tới trên gương Gi bằng 300. Tìm góc α để cho tia tới trên gương G1 và tia phản xạ trên gương G2 vuông góc với nhau:

Tại I, theo định luật phản xạ, ta có:

\(\widehat {SIN} = \widehat {NIJ} = {30^0} \Rightarrow \left\{ \begin{array}{l}
\widehat {JIO} = \widehat {NIO} - \widehat {NIJ} = 90 - 30 = {60^0}\\
\widehat {KIJ} = 2.\widehat {SIN} = 2.30 = {60^0}\,\,\,\left( 1 \right)
\end{array} \right.\)

Trong tam giác IJO, ta có:

\(\begin{array}{l}
\widehat {IJO} = {180^0} - \widehat {JIO} - \widehat {IOJ} = {180^0} - {60^0} - \alpha = {120^0} - \alpha \\
\Rightarrow \widehat {NJI} = {90^0} - \widehat {IJO} = {90^0} - \left( {{{120}^0} - \alpha } \right) = \alpha - {30^0}
\end{array}\)

Tại K, theo định luật phản xạ, ta có:

\(\widehat{IJN}=\widehat{NJK}\Rightarrow \widehat{KJI}=2.\widehat{NJK}=2\alpha -60\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta được: ..

Trong tam giác IKJ, ta có: \(\widehat{IKJ}={{180}^{0}}-\left( \widehat{KIJ}+\widehat{KJI} \right)={{180}^{0}}-2\alpha \)

Để tia tới SI trên gương G1 vuông góc với tia phản xạ JR trên gương G2 thì:

\(\widehat{IKJ}={{90}^{0}}\Leftrightarrow {{180}^{0}}-2\alpha ={{90}^{0}}\Rightarrow \alpha ={{45}^{0}}\)