-
Câu hỏi:
Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được \(\widehat {BAC} = 65^\circ \). Chiều cao của cây gần với kết quả nào nhất sau đây?
-
A.
38m;
-
B.
39m;
-
C.
19m;
-
D.
20m.
Lời giải tham khảo:
Đáp án đúng: A
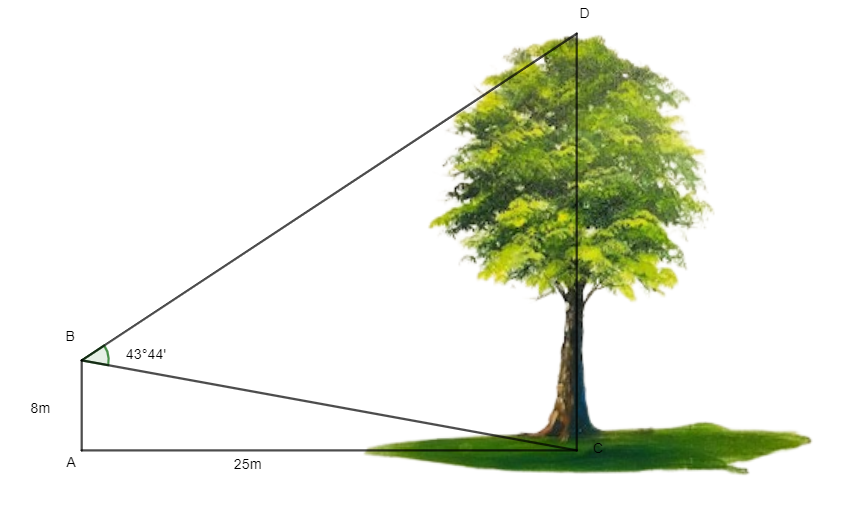
Đặt các điểm A, B, C, D như trên hình vẽ, khi đó:
Xét tam giác ABC vuông tại A, có:
\(\tan \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{{25}}{8} \Rightarrow \widehat {ABC} \approx 72^\circ 15'\)
\( \Rightarrow \widehat {ABD} = \widehat {ABC} + \widehat {CBD} \approx 72^\circ 15' + 43^\circ 44' = 115^\circ 59'\)
Vì AB // CD nên \(\widehat {BDC} = 180^\circ - \widehat {ABD} \approx 64^\circ 1'\)
Xét tam giác BDC, có:
\(\begin{array}{l}
\frac{{BC}}{{\sin \widehat {CBD}}} = \frac{{BC}}{{\sin \hat D}}\\
\Leftrightarrow BC = \frac{{BC.\sin \hat D}}{{\sin \widehat {CBD}}} = \frac{{\sqrt {689} .\sin 64^\circ 1'}}{{\sin 43^\circ 44'}} \approx 20,2
\end{array}\)Vậy độ dài cây khoảng 20m.
Đáp án đúng là: A
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?
- Cho mệnh đề chứa biến P(n): “n2 chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:
- Mệnh đề phủ định của mệnh đề “Phương trình ax2 + bx + c = 0 (a ≠ 0) vô nghiệm” là:
- Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm A∩B
- Cho biết A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?
- Số phần tử của tập hợp A = {k2 + 1| k ∈ ℤ, |k| ≤ 2} bằng
- Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là
- Hình vẽ cho sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
- Lớp 10A1 có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A1 là:
- Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?
- Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?
- Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?
- Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:
- Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°
- Cho tam giác ABC, ta có các đẳng thức:
- Cho điểm M(x0; y0) nằm trên đường tròn đơn vị thỏa mãn \(\widehat {xOM} = \alpha \). Khi đó phát biểu nào dưới đây là sai?
- Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, ha, hb, hc lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.
- Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:
- Cho tam giác ABC có BC = 50 cm, ˆ B = 65 ° , ˆ C = 45 ° B^=65°,C^=45°. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét). Chu vi của tam giác ABC là:
- Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được \(\widehat {BAC} = 65^\circ \). Chiều cao của cây gần với kết quả nào nhất sau đây?
- Đẳng thức nào cho sau đây, mô tả đúng hình vẽ bên?
- Cho hình chữ nhật ABCD. Hãy chọn khẳng định đúng.
- Cho hình bình hành ABCD với điểm K thỏa mãn \(\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{AB}\) thì
- Cho tam giác đều ABC có AB = a, M là trung điểm của BC. Khi đó \(\left| \overrightarrow{MA}+\overrightarrow{AC} \right|\) bằng
- Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?
- Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:
- Phát biểu nào sau đây là sai về vecto?
- Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?
- Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \) bằng
- Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ 2 ( −−→ H A − −−→ H C ) 2HA→−HC→bằng
- Kí hiệu nào sau đây để chỉ \(\sqrt 5 \) không phải là số hữu tỉ?
- Một nhóm các học sinh lớp 10H giỏi Toán hoặc giỏi Văn. Trong đó, có 5 bạn giỏi Toán; 7 bạn giỏi Văn và 2 bạn giỏi cả hai môn. Hỏi nhóm đó có bao nhiêu học sinh?
- Cho tập A = (−∞; 1] và B = (m; +∞). Tất cả các giá trị của m để A ∩ B ≠ ∅ là:
- Cho A = (−20; 20) và B = [2m – 4; 2m + 2) (m là tham số). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để B ⊂ A?
- Cho hai tập hợp A = [−1; 3), B = [a; a + 3]. Với giá trị nào của a thì A ∩ B = \(\emptyset \)?
- Trong các cặp số đã cho sau đây, cặp nào không là nghiệm của bất phương trình: 2x + y < 1?
- Cặp số sau đây (2; 3) là nghiệm của bất phương trình nào sau đây?
- Điểm nào cho sau đây thuộc miền nghiệm của hệ bất phương trình sau \(\left\{ \begin{array}{l}2x - 5y - 1 > 0\\2x + y + 5 > 0
- Phần nửa mặt phẳng tô đậm (không kể đường thẳng d) là miền nghiệm của bất phương trình nào?
- Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) trong hình dưới đây là miền nghiệm của bất phương trình nào?

