-
Câu hỏi:
Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I. Biết AB=20cm, AC=28cm, BC=24cm. Khi đó IA bằng bao nhiêu cm?
-
A.
32cm
-
B.
20cm
-
C.
28cm
-
D.
35cm
Lời giải tham khảo:
Đáp án đúng: D
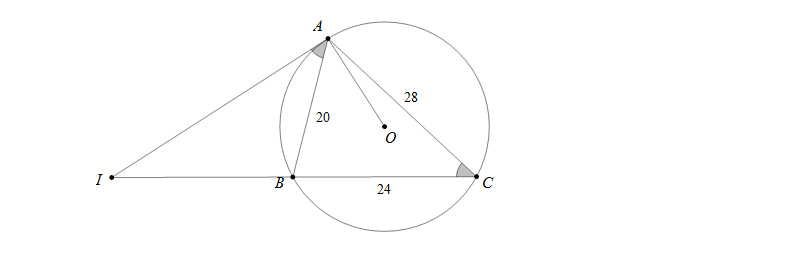
Đặt \(IA=x, IC=y\). Ta có \(\bigtriangleup BAI \sim \bigtriangleup ACI\) (g.g) \(\Rightarrow \frac{AI}{CI}=\frac{BI}{AI}=\frac{AB}{CA}\)
Suy ra \(\frac{x}{y}=\frac{y-24}{x}=\frac{20}{28}=\frac{5}{7}\)
Từ đây ta có hệ \(\left\{\begin{array}{l} 7x=5y \\ 5x=7(y-24) \end{array}\right.\Rightarrow \left\{\begin{array}{l} x=35 \\ y=49 \end{array}\right.\)
Khi đó IA=35cm.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Khẳng định nào sau đây các em cho là sai:
- Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I. Biết AB=20cm, AC=28cm, BC=24cm. Khi đó IA bằng bao nhiêu cm?
- Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại AA của đường tròn (O′) cắt (O) tại CC và đối với đường tròn (O) cắt (O′) tại D
- Trong các khẳng định sau, khẳng định nào đúng:
- Cho đường tròn (O;R), điểm A nằm ngoài đường tròn và OA=2R. Từ A vẽ hai tiếp tuyến AB,AC đến đường tròn (O)




