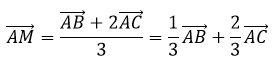-
Câu hỏi:
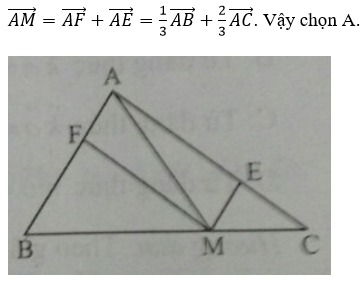
Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 2MC. Khi đó khẳng định nào sau đây là đúng?
-
A.
\(\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
-
B.
\(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
-
C.
\(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AC} \)
-
D.
\(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
Lời giải tham khảo:
Đáp án đúng: A
Cách 1. Qua M kẻ đường thẳng song song với AB, AC tạo thành hình bình hành MEAF. Áp dụng định lí Ta – lét và quy tắc hình bình hành ta có:
Cách 2. Áp dụng quy tắc trung điểm mở rộng MB→=-2MC→ nên
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Tìm khẳng định sai:
- Cho hình bình hành ABCD tâm O. Mệnh đề sai là?
- Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Vectơ vec{CA}-vec{HC} có độ dài là?
- Cho hình bình hành ABCD có AD=2cm, AB=4cm, BD=5cm. Giá trị của |vec{BA}-vec{DA}| là:
- Cho vectơ \(\overrightarrow a ,\overrightarrow b \) và các số thực m, n, k. Khẳng định nào sau đây là đúng?
- Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \). Biết rằng B nằm giữa A và C.
- Cho ba ABC với các trung tuyến AM, BN, CP. Khẳng định nào sau đây sai?
- Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 2MC. Khi đó khẳng định nào sau đây là đúng?
- Cho tam giác ABC và đường thẳng d. Vị trí của điểm M trên d sao chocó giá trị nhỏ nhất là:
- Cho tứ giác ABCD; X là trọng tâm của tam giác BCD, G là trọng tâm tứ giác ABCD. Khẳng định nào sau đây đúng?
VIDEO
YOMEDIA
ADMICRO
