-
Câu hỏi:
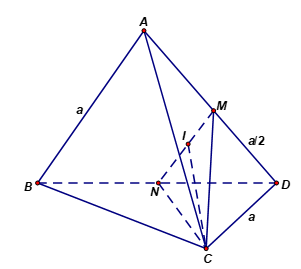
Cho hình tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M\) là trung điểm của cạnh \(AD\). Tính khoảng cách giữa 2 đường thẳng \(AB\) và \(CM\) theo \(a\)?
-
A.
\(\frac{a\sqrt{33}}{11}\).
-
B.
\(\frac{a}{\sqrt{33}}\).
-
C.
\(\frac{a}{\sqrt{22}}\).
-
D.
\(\frac{a\sqrt{22}}{11}\).
Lời giải tham khảo:
Đáp án đúng: D
Gọi \(N\) là trung điểm của \(BD\), \(I\) là trung điểm của \(MN\).
Tam giác \(CMN\) là tam giác cân có \(CM=CN=\frac{a\sqrt{3}}{2};\,\,MN=\frac{a}{2}\)\( \Rightarrow CI=\frac{a\sqrt{11}}{4}\) nên có diện tích \({{S}_{CMN}}=\frac{{{a}^{2}}\sqrt{11}}{16}\).
Thể tích khối tứ diện đều cạnh \(a\) là \(\frac{{{a}^{3}}\sqrt{3}}{12}\).
Vậy thể tích khối tứ diện \(M.NCD\) là \({{V}_{M.NCD}}\)\( =\frac{1}{4}.\frac{{{a}^{3}}\sqrt{3}}{12}\)\( =\frac{{{a}^{3}}\sqrt{3}}{48}\).
Vậy \(d\left( D,\,\left( CMN \right) \right)=d\left( A,\,\left( CMN \right) \right)\)\( =d\left( AB,\,CM \right)\)\( =\frac{3{{V}_{M.CDN}}}{{{S}_{CMN}}}\)\( =\frac{\frac{3.{{a}^{3}}\sqrt{2}}{48}}{\frac{{{a}^{2}}\sqrt{11}}{16}}\)\( =\frac{a\sqrt{22}}{11}\).
Vì khối lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{{a}^{3}}\)\( ={{\left( 2a \right)}^{3}}\) nên cạnh của hình lập phương là \(2a\).
Chọn D
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho CSC \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=2\) và số hạng thứ tư \({{u}_{4}}=17\). Công sai của cấp số cộng đã cho bằng?
- TXĐ của hàm số \(y={{\left( 2-x \right)}^{\frac{1}{2}}}\) là?
- Có tất cả bao nhiêu cách chọn ra 2 học sinh gồm nam và nữ từ nhóm \(10\) học sinh gồm \(4\) nam và \(6\) nữ?
- Nghiệm của phương trình sau \({{\log }_{2}}\left( x-1 \right)=4\) là?
- Cho khối lăng trụ có diện tích đáy là \(B=3\) và chiều cao \(h=4\). Thể tích của khối lăng trụ này bằng?
- Cho khối cầu có bán kính \(R=6\). Tính thể tích khối cầu bằng?
- Với \(a,b\) là các số thực dương tùy ý, ta có \(\log \left( {{a}^{5}}{{b}^{10}} \right)\) bằng?
- Cho hình trụ có bán kính \(r=2\) và chiều cao \(h=3\). Diện tích xung quanh Sxq của hình trụ này bằng?
- Cho HS \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau: Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
- Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và dấu của đạo hàm cho bởi công thức sau: Hàm số \(f\left( x \right)\) có mấy điểm cực trị?
- Đường TCĐ của đồ thị hàm số \(y=\frac{x}{x-1}\) là?
- Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ: Số nghiệm của phương trình \(2f\left( x \right)+1=0\) là?
- Tập nghiệm của bất phương trình sau \({{5}^{2x+1}}\le 25\) là?
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
- Cho HS \(f\left( x \right)\), \(g\left( x \right)\) liên tục trên \(\left[ 0;\,2 \right]\) và \(\int\limits_{0}^{2}{f\left( x \right)\text{d}x}=2\), \(\int\limits_{0}^{2}{g\left( x \right)\text{d}x}=-2\). Tính \(\int\limits_{0}^{2}{\left[ 3f\left( x \right)+g\left( x \right) \right]\text{d}x}\)?
- Trong không gian \(Oxyz,\) hình chiếu vuông góc của điểm \(M\left( 3;\,1;\,2 \right)\) lên trục \(Oy\) là
- Trong không gian \(Oxyz,\) cho mp \(\left( P \right):\,2x+y-z+3=0\). Điểm nào sau đây không thuộc mặt phẳng \(\left( P \right)\)?
- Cho các số phức sau \(z=2+i\) và \(\omega =3-2i\). Phần ảo của số phức \(z+2\omega \) bằng?
- Cho số phức \(z=2i+1\). Điểm nào dưới đây là điểm biểu diễn của số phức \(z\) trên mặt phẳng tọa độ?
- Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+1=0\). Hãy tính
- Cho số phức sau \(z=2+i\). Mô đun của số phức \(\text{w}=\overline{z}+3z\) bằng?
- Cho hàm số \(f\left( x \right)\) thỏa mãn \({f}'\left( x \right)={{x}^{2}}\left( x-1 \right),\forall x\in
- Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mp \(\left( ABC \right)\), \(SA=1\) và đáy \(ABC\) là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\)?
- Biết rằng \({{\log }_{3}}4=a\) và \(T={{\log }_{12}}18\). Phát biểu nào là đúng?
- GTLN của hàm số \(y=\frac{{{x}^{2}}-2x+1}{x+2}\) trên đoạn \(\left[ 0\,;\,3 \right]\) bằng?
- Tập nghiệm của bất phương trình sau \(\log _{2}^{2}\left( 2x \right)+1\le {{\log }_{2}}\left( {{x}^{5}} \right)\) là?
- Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi các đồ thị sau \(y={{x}^{2}}-2x\), \(y=0\) trong mặt phẳng \(Oxy\). Quay hình \(\left( H \right)\) quanh trục hoành ta được một khối tròn xoay có thể tích bằng?
- Xét tích phân \(I=\int_{0}^{1}{{{e}^{\sqrt{2x+1}}}\text{d}x}\), nếu đặt \(u=\sqrt{2x+1}\)thì giá trị của \(I\) bằng?
- Cho \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức phân biệt của phương trình sau \({{z}^{2}}-4z+13=0\). Tính \({{\left| {{z}_{1}}+i \right|}^{2}}+{{\left| {{z}_{2}}+i \right|}^{2}}\)?
- Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a\), cạnh bên bằng \(3a\). K/c từ \(A\) đến mp \(\left( SCD \right)\) bằng?
- Trong không gian \(Oxyz\), cho điểm \(A\left( 1;1;-2 \right)\) và đt \(d:\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-2}\). Đường thẳng qua \(A\) và song song với \(d\) có phương trình tham số là?
- Trong không gian \(Oxyz\), cho \(A\left( 1;1;-2 \right)\); \(B\left( 2;0;3 \right)\); \(C\left( -2;4;1 \right)\). Mp
- TXĐ của hàm số \({y=\sqrt{\log _{\frac{1}{2}}\left(x^{2}+7 x\right)+3}}\) là?
- Cho 6 HS gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của 3 lớp A, B, C?
- Cho hình tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M\) là trung điểm của cạnh \(AD\). Tính khoảng cách giữa 2 đường thẳng \(AB\) và \(CM\) theo \(a\)?
- Cho HS \(f\left( x \right)\) thỏa mãn \(f\left( 0 \right)=\frac{2}{3}\) và \(\left( \sqrt{x}+\sqrt{x+1} \right).{f}'\left( x \right)=1,\forall x\ge -1\). Biết \(\int\limits_{0}^{1}{f\left( x \right)dx}=\frac{a\sqrt{2}+b}{15}\) với \(a,b\in \mathbb{Z}\). Tính \(T=a+b\)?
- Biết rằng đồ thị \((H):y=\frac{{{x}^{2}}+2x+m}{x-2}\) có 2 điểm cực trị \(A,B\). Hãy tính k/c từ gốc tọa độ đến đường thẳng \(AB\)?
- Cho hình trụ có bán kính đáy bằng \(a\sqrt{3}\). Cắt hình trụ bởi 1 mặt phẳng song song với trục, cách trục 1 khoảng bằng a ta được thiết diện là một hình vuông. Thể tích khối trụ đó bằng?
- Có tất cả bao nhiêu số phức \(z\) thỏa mãn \(\left( {{z}^{2}}-2z+7 \right)\left( z-2{{\overline{z}}^{2}} \right)=0\)?
- Cho HS \({y=x^{3}-3 m x^{2}+12 x+3 m-7}\) với \({m}\) là tham số. Số các giá trị nguyên của \({m}\) đề hàm số đã cho đồng biến trên \({\mathbb{R}}\) là?
- Cho hàm số sau . Biết \(\int\limits_{\frac{1}{e}}^{e}{\frac{f\left( \ln x \right)}{x}dx}=a\sqrt{3}+b\ln 2+c\) với \(a,b,c\in \mathbb{Q}\). Giá trị của \(a+b+6c\) bằng?
- Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\log _{3}^{2}x-m{{\log }_{9}}{{x}^{2}}+2-m=0\) có nghiệm \(x\in \left[ 1;9 \right]\)?
- Cho HS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đồ thị \({f}'\left( x \right)\) như hình: Số điểm cực tiểu của hàm số \(g\left( x \right)=f\left( -{{x}^{2}}+x \right)\) là?
- Cho hệ tọa độ \({O x y z}\), cho tam giác \({A B C}\) có \({A B=2 A C}\) và điểm \(M(2 ; 0 ; 4)\). Biết điểm \(B\) thuộc đường thẳng \(d: \frac{x}{1}=\frac{y}{1}=\frac{z}{1}\), điểm \(C\) thuộc mặt phẳng \((P): 2 x+y-z-2=0\) và \({A M}\) là phân giác trong của tam giác \({A B C}\) kẻ từ \(A(M \in B C)\). Phương trình đường thẳng \({B C}\) là?
- Xét hàm số \(f\left( x \right)=\left| \frac{mx-2\sqrt{x+4}}{2x+4} \right|\) với \(m\) là tham số thực. Có
- Trong không gian \(Oxyz\) cho mặt cầu \((S):(x+2)^{2}+y^{2}+(z+5)^{2}=24\) cắt mp \((\alpha): x+y+4=0\) theo giao tuyến là đường tròn \((C)\). Điểm \(M\) thuộc \((C)\) sao cho khoàng cách từ \(M\) đến \(A(4 ;-12 ; 1)\) nhỏ nhất có tung độ bằng?
- Cho hàm số bậc bốn \(y=f\left( x \right)\). Biết hàm số \(y={f}'\left( 1+x \right)\) có đồ thị như
- Có tất cả bao nhiêu bộ \(\left( x;y \right)\) với \(x,y\) nguyên và \(1\le x,y\le 2020\) thỏa mãn \(\left( xy+2x+4y+8 \right){{\log }_{3}}\left( \frac{2y}{y+2} \right)\le \left( 2x+3y-xy-6 \right){{\log }_{2}}\left( \frac{2x+1}{x-3} \right)\)?
- Cho số phức \(z\) thỏa mãn \(\left| z+1 \right|\ge 1\). Gọi GTLN và GTNN của biểu thức \(P=\left| \frac{\left( 1+i \right)z+i+2}{z+1} \right|\) lần lượt là \(M\) và \(m\). Khi đó giá trị của \(\left( {{M}^{2}}+{{m}^{2}} \right)\) bằng?
- Cho khối lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), \(AB=2a\) và góc tạo bởi 2 mặt phẳng \(\left( AB{C}' \right)\) và \(\left( ABC \right)\) bằng \(60{}^\circ \). Gọi \(M,N\) lần lượt là trung điểm của \({A}'{C}'\) và \(BC\). Mặt phẳng \(\left( AMN \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng?

.PNG)