-
Câu hỏi:
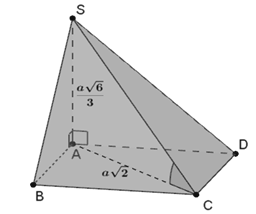
Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình vuông cạnh bằng \(a\) và \(SA\bot \left( ABCD \right).\) Biết \(SA=\frac{a\sqrt{6}}{3}\). Tính góc giữa \(SC\) và \(\left( ABCD \right).\)
-
A.
\({{30}^{0}}.\)
-
B.
\({{60}^{0}}.\)
-
C.
\({{75}^{0}}.\)
-
D.
\({{45}^{0}}.\)
Lời giải tham khảo:
Đáp án đúng: A
Tứ giác \(ABCD\) là hình vuông cạnh \(a\) nên \(AC=a\sqrt{2.}\)
\(SA\bot \left( ABCD \right)\Rightarrow AC\) là hình chiếu vuông góc của \(SC\) lên \(\left( ABCD \right)\Rightarrow \widehat{SCA}\) là góc giữa \(SC\) và \(\left( ABCD \right).\)
Tam giác \(SAC\) vuông tại \(A\) nên \(\tan \widehat{SCA}=\frac{SA}{AC}=\frac{a\sqrt{6}}{3}.\frac{1}{a\sqrt{2}}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{SCA}={{30}^{0}}.\)
Chọn đáp án A.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho tứ diện \(ABCD\) có cạnh \(AB\), \(BC\), \(BD\) bằng nhau và vuông góc với nhau từng đôi một
- Cho tam giác \(ABC\) vuông cân tại \(A\) và \(BC=a\). Trên đường thẳng qua \(A\) vuông góc với
- Cho tứ diện \(ABCD\) có cạnh \(AB,\text{ }BC, BD\) vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng ?
- Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cạnh huyền \(BC=a\).
- Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh bằng \(a\) và \(SA\bot \left( ABCD \right)\). Biết \(SA=\frac{a\sqrt{6}}{3}\)
- Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu
- Cho hình thoi \(ABCD\) có tâm \(O\), \(AC=2a;BD=2\text{A}C\). Lấy điểm \(S\) không thuộc
- Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu vuông góc của \(S\)
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\bot (ABCD),SA=a\sqrt{6}.\)
- Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình vuông cạnh bằng \(a\) và