-
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \frac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
-
A.
\(h = \frac{{\sqrt 3 a}}{2}\)
-
B.
\(h = \frac{{a\sqrt 3 }}{7}\)
-
C.
\(h = \frac{{a\sqrt {21} }}{2}\)
-
D.
\(h = \frac{{3a}}{5}\)
Lời giải tham khảo:
Đáp án đúng: A
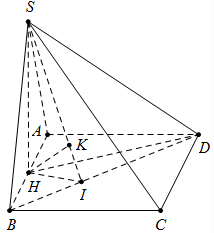
Từ H kẻ HI vuông góc với BD \(\left( {I \in BD} \right)\) và \(HK \bot SI\)
Suy ra \(HK \bot \left( {SBD} \right).\)
Ta có:
\(SH = \sqrt {S{D^2} - H{D^2}} = a\sqrt 3\) và
\(HI = \frac{{AC}}{4} = \frac{{a\sqrt 2 }}{4}\)
Suy ra \(HK = \frac{{SH.IH}}{{\sqrt {S{H^2} + I{H^2}} }} \)
\(= \frac{{\frac{{{a^2}\sqrt 6 }}{4}}}{{\frac{{5a\sqrt 2 }}{4}}} = \frac{{a\sqrt 3 }}{5}\)
Do đó chiều cao của khối chóp H.SBD là:
\(h = \frac{{a\sqrt 3 }}{5}.\)
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1
- Cho khối lăng trụ ABC.A’B’C’ có thể tích V. Tính thể tích \(V_1\) của khối tứ diện A’B’C'C
- Cho hình chóp S.ABC có đáy là tam giác vuông cân có cạnh huyền là 4a và thể tích bằng \( a^3 \). Tính chiều cao h của khối chóp S.ABC
- Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150 m, cạnh đáy dài 220 m
- Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \dfrac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \(a^3\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
- Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Biết AC’ tạo với mặt phẳng (A'B'C) một góc 60^0 và AC' = 4a.
- Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh bằng a, góc \(\widehat{A}\) bằng \(60^0\) và cạnh bên AA’ = 2a. Tính thể tích V của khối hộp ABCD.A’B’C’D’.
- Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của cạnh SD. Biết rằng khối chóp S.ABCD có thể tích bằng \(a^3\) và tam giác MAC là tam giác đều cạnh a, hãy tính khoảng cách d từ điểm S đến mặt phẳng (MAC).
- Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA=a. Điểm M thuộc cạnh SA sao cho \(\frac{{SM}}{{SA}} = k\). Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

