-
Câu hỏi:
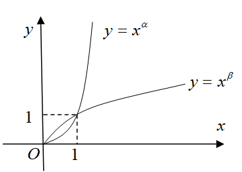
Cho \(\alpha \),\(\beta \) là các số thực. Đồ thị các hàm số sau \(y={{x}^{\alpha }}\),\(y={{x}^{\beta }}\) trên khoảng \(\left( 0;+\infty \right)\) được cho trong hình. Khẳng định nào đúng?
-
A.
\(0 < \beta < 1 < \alpha \).
-
B.
\(\alpha < 0 < 1 < \beta \).
-
C.
\(\beta < 0 < 1< \alpha \).
-
D.
\(0 < \alpha < \beta < 1\).
Lời giải tham khảo:
Đáp án đúng: A
Với x0 > 1 ta có:
\(\begin{align} & x_{0}^{\alpha }>1\Rightarrow \alpha >0;x_{0}^{\beta }>1\Rightarrow \beta >0 \\ & x_{0}^{\alpha }>x_{0}^{\beta }\Rightarrow \alpha >\beta \\ \end{align}\)
Mặt khác, dựa vào hình dáng đồ thị ta suy ra \(\alpha >1\) và \(\beta <1\).
\(\Rightarrow 0<\beta <1<\alpha \)
Chọn D
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho hình nón có bán kính đáy \(r=\sqrt{3}\) và độ dài đường sinh \(l=4\). Tính diện tích xung quanh
- Cho một người gửi \(100\) triệu đồng vào ngân hàng với lãi suất \(0,4%/\) tháng. Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau \(6\) tháng, người đó được lĩnh số tiền ( cả vốn ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi?
- Hàm số sau đây \(f(x)={{\log }_{2}}\left( {{x}^{2}}-2 \right)\) có đạo hàm là?
- Cho hình chóp tứ giác đều có cạnh đáy bằng \(2a\), cạnh bên bằng \(3a\). Gọi \(\alpha \)là góc
- Cho \(\alpha \),\(\beta \) là các số thực. Đồ thị các hàm số sau \(y={{x}^{\alpha }}\),\(y={{x}^{\beta }}\) trên khoảng \(\left( 0;+\infty \right)\) được cho trong hình. Khẳng định nào đúng?
- Cho \(a,b\) là các số thực thỏa mãn \({{\left( \sqrt{2}-1 \right)}^{a}}>{{\left( \sqrt{2}-1 \right)}^{b}}\).
- Cho hàm số \(y=f\left( x \right)\) có đạo hàm \({f}'\left( x \right)=(x-1)({{x}^{2}}-3x+3)\)\(\forall x\in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào?
- Cho biết hàm số \(y={{x}^{4}}-2\) nghịch biến trên khoảng nào?
- Cho \(a\) là số thực dương khác 1. Giá trị của biểu thức sau \({{\log }_{a}}\left( \frac{{{a}^{2}}\sqrt[3]{{{a}^{2}}}\sqrt[5]{{{a}^{4}}}}{\sqrt[15]{{{a}^{7}}}} \right)\) bằng?
- Thể tích khối hộp chữ nhật có 3 kích thước bằng \(a,\,a\sqrt{2},\,a\sqrt{3}\) là?
- Hàm số \(y=\frac{1}{3}{{x}^{3}}+{{x}^{2}}-3x+1\) đạt CT tại điểm?
- Phương trình sau \({{\log }_{2}}\left( x+1 \right)=4\) có nghiệm là?
- Có bao nhiêu giao điểm của ĐTHS \(y={{x}^{3}}+3x-3\) với trục \(Ox\)?
- Cho một vật chuyển động theo quy luật \(s=\frac{1}{3}{{t}^{3}}-{{t}^{2}}+9t\) với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
- Trên đoạn \(\left[ -2;1 \right]\), hàm số \(y={{x}^{3}}+3{{x}^{2}}-1\) đạt GTNN tại điểm?
- Đạo hàm của hàm số sau \(y={{4}^{{{x}^{2}}+x+1}}\) là?
- Cho đa giác đều \(P\) gồm 16 đỉnh. Chọn ngẫu nhiên 1 tam giác có 3 đỉnh là đỉnh của \(P\). Tính xác suất để tam giác chọn được là tam giác vuông?
- Đường TCĐ của đồ thị hàm số \(y=\frac{3x+2022}{x-1}\) có phương trình là?
- Biết rằng đồ thị hàm số \(y={{x}^{4}}-2a{{x}^{2}}+b\) có 1 điểm cực trị là \(\left( 1\,;\,2 \right)\). Tính k/c giữa điểm cực đại và điểm cực tiểu của đồ thị hàm số đã cho?
- Cho hàm bậc 3 sau \(y\,=\,f\left( x \right)\) có đồ thị đạo hàm \(y={f}'\left( x \right)\) như hình: Hàm số đã cho nghịch biến trên khoảng?
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mp đáy, \(SA=a\). Gọi \(M\) là trung điểm của \(CD\). Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( SAB \right)\)?
- Tính thể tích \(V\) của khối chóp có diện tích đáy bằng \(B\) và chiều cao bằng \(h\)?
- Cho khối lăng trụ tam giác\(ABC.{A}'{B}'{C}'\), biết rằng thể tích khối chóp \({A}'.A{B}'{C}'\) bằng
- Một phòng có 12 người. Cần lập một tổ đi công tác 3 người, 1 người làm tổ trưởng, 1 người làm tổ phó và 1 người là thành viên. Hỏi có bao nhiêu cách lập?
- Cho hình nón có chiều cao và bán kính đáy bằng \(1\). Mặt phẳng \(\left( P \right)\) qua đỉnh của hình nón và cắt đáy theo dây cung có độ dài bằng \(1\). Khoảng cách từ tâm của đáy tới mặt phẳng \(\left( P \right)\) bằng?
- Cho khối chóp \(S.ABCD\) có thể tích \(V=32\). Gọi \(M,N,P,Q\) lần lượt là trung điểm \(SA,SB,SC,SD\). Tính thể tích khối đa diện \(MNPQABC\text{D}\) bằng?
- Tìm TXĐ \(D\) của hàm số \(y={{\left( {{x}^{2}}-3x \right)}^{-4}}\)?
- Đường thẳng nào dưới đây là TCNg của đồ thị hàm số \(y=\frac{2x+1}{x+5}\)?
- Với \(a\) là số thực thỏa mãn \(0
- Cho biết hình tứ diện đều có tất cả bao nhiêu mặt phẳng đối xứng?
- Trong các hàm số dưới đây, hàm số nào đồng biến trên \(\mathbb{R}\)?
- Biết phương trình sau \(\log _{9}^{2}x+{{\log }_{3}}\frac{x}{27}=0\) có 2 nghiệm \({{x}_{1}},\,\,{{x}_{2}}\) với \({{x}_{1}}
- Hãy tính thể tích \(V\) của khối lăng trụ tam giác đều có tất cả các cạnh bằng \(a\)?
- Tổng các nghiệm của phương trình sau \({{3}^{{{x}^{2}}-3x}}=\frac{1}{9}\) bằng?
- Cho hàm số \(y=f\left( x \right)\) có BBT như sau: Số điểm cực trị của hàm số \(g\left( x \right)={{f}^{3}}\left( x \right)+3{{f}^{2}}\left( x \right)+2020\) là?
- Cho hàm số \(y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\) \(\left( a,b,c,d\in \mathbb{R} \right)\) có đồ
- Giả sử phương trình \({{25}^{x}}+{{15}^{x}}={{6.9}^{x}}\) có 1 nghiệm duy nhất được viết dưới dạng \(\frac{a}{{{\log }_{b}}c-{{\log }_{b}}d}\), với \(a\) là số nguyên dương và \(b,c,d\) là các số nguyên tố. Tính \(S={{a}^{2}}+b+c+d\)?
- Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( -8\,;\,+\infty \right)\) để phương trình sau \({{x}^{2}}+x\left( x-1 \right){{2}^{x+m}}+m=\left( 2{{x}^{2}}-x+m \right){{.2}^{x-{{x}^{2}}}}\) có nhiều hơn 2 nghiệm phân biệt ?
- Có tất cả bao nhiêu bộ 3 số thực \(\left( x,y,z \right)\) thỏa mãn đồng thời các điều kiện dưới đây \({{2}^{\sqrt[3]{{{x}^{2}}}}}{{.4}^{\sqrt[3]{{{y}^{2}}}}}{{.16}^{\sqrt[3]{{{z}^{2}}}}}=128\) và \({{\left( x{{y}^{2}}+{{z}^{4}} \right)}^{2}}=4+{{\left( x{{y}^{2}}-{{z}^{4}} \right)}^{2}}\)?
- Hàm số nào sau đây có đồ thị như hình?
- Cho hình chóp tứ giác đều có độ dài cạnh đáy bằng \(a\) và chiều cao bằng \(2a.\) Tính theo
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB=a\), \(AD=2a\), \(SA\bot (ABCD)\) và \(SA=a\). Gọi \(N\) là trung điểm của \(CD\). Tính k/c từ \(A\) đến mp \(\left( SBN \right)\)?
- Cho hàm số \(y=f\left( x \right)\) có BBT như sau: Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(g\left( x \right)=\left| f\left( x \right)-3m \right|\) có \(5\) điểm cực trị?
- Khối tròn xoay sinh bởi 1 tam giác đều cạnh \(a\) (kể cả điểm trong) khi quay quanh 1 đường thẳng chứa 1 cạnh của tam giác đó có thể tích bằng?
- Cho \(y=f\left( x \right)\)có đồ thị \({f}'\left( x \right)\) như hình: GTNN của hàm số \(g\left( x \right)=f\left( x \right)+\frac{1}{3}{{x}^{3}}-x\) trên đoạn \(\left[ -1;2 \right]\) bằng?
- Tìm số các giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( -20;20 \right)\) để hàm số sau \(f\left( x \right)=\frac{1}{7}{{x}^{7}}+\frac{6}{5}{{x}^{5}}-\frac{{{m}^{3}}}{4}{{x}^{4}}+\left( 5-{{m}^{2}} \right){{x}^{3}}-3m{{x}^{2}}+10x+2020\) đồng biến trên \(\left( 0;1 \right)\)?
- Cho khối chóp \(S.ABC\) có \(\widehat{ASB}=\widehat{BSC}=\widehat{CSA}=60{}^\circ ,\) \(SA=a,\) \(SB=2a,\)
- Cho hàm số \(y=f\left( x \right)\). Đồ thị hàm số \(y={f}'\left( x \right)\) như hình. Hỏi hàm số \(g\left( x \right)=f\left( {{x}^{2}}-5 \right)\) có bao nhiêu khoảng nghịch biến?
- Tìm số giá trị nguyên thuộc đoạn \(\left[ -2022;\,2022 \right]\) của tham số \(m\) để đồ thị
- Cho lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có đáy là tam giác vuông tại \(A\), \(AB=2;AC=\sqrt{3}\). Góc