-
Câu hỏi:
Cho 2 đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\angle xOy = \dfrac{2}{3}\angle xOy'\). Tính số đo \(\angle xOy'\)?
-
A.
\({36^0}\)
-
B.
\({72^0}\)
-
C.
\({108^0}\)
-
D.
\({18^0}\)
Lời giải tham khảo:
Đáp án đúng: C
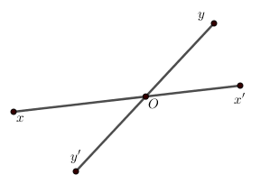
Vì \(\angle xOy\) và \(\angle x'Oy\) là hai góc kề bù nên \(\angle xOy + \angle x'Oy = {180^0}\)
Mà \(\angle xOy = \dfrac{2}{3}\angle x'Oy\)
Suy ra \(\dfrac{2}{3}\angle x'Oy + \angle xOy' = {180^0}\)
\(\dfrac{5}{3}\angle xOy' = {180^0}\)
\(\begin{array}{l}\angle xOy' = {180^0}:\dfrac{5}{3} = {180^0}.\dfrac{3}{5}\\\angle xOy' = {108^0}\end{array}\)
Vậy \(\angle xOy' = {108^0}\)
Chọn C.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho 1 đường thẳng cắt 2 đường thẳng song song. Khi đó số cặp góc đồng vị bằng nhau được tạo thành là?
- Kết quả của phép tính sau \(\left( {\dfrac{2}{3} - \dfrac{5}{4}} \right):\dfrac{{21}}{{12}}\) là?
- Phân số biểu diễn số hữu tỉ -0,6 là?
- Giá trị của x trong biểu thức: \( - {x^3} = 27\) là?
- Cho \(\widehat {xOy} = 40^\circ \). Trên tia \(Ox,Oy\) lần lượt lấy điểm A, B khác O. Từ A vẽ đường
- Cho 3 đường thẳng phân biệt a,b,c. Hai đường thẳng a và b song song với nhau khi nào?
- Số \(\dfrac{{ - 4}}{{ - 5}}\) được biểu diễn trên trục số bởi hình nào dưới đây?
- Số hữu tỉ x thoả \(x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\) là?
- Tính \( - 23,\left( 2 \right) + \dfrac{3}{7} + 13,\left( 2 \right) - \dfrac{{10}}{7}\)?
- Cho 2 đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\angle xOy = \dfrac{2}{3}\angle xOy'\). Tính số đo \(\angle xOy'\)?
- Cho tia On là tia phân giác của \(\angle mOt\). Biết \(\angle mOn = {70^^\circ }\), tính số đo của \(\angle mOt\)?
- Cho ĐL: “Nếu hai đường thẳng song song cắt đường thẳng thứ 3 thì hai góc đồng vị bằng nhau' (xem hình vẽ dưới đây). Giả thiết của định lí là?
- Số hữu tỉ là..?
- Giá trị x thỏa \( - 8{x^2} + 50 = 0\) là?
- Kết quả của phép tính: \(\dfrac{{{3^5}{{.4}^3}}}{{{9^2}{{.8}^2}}}\) là?
- Trên hình, 2 góc A1 và B3 ở vị trí gì?
- Cho \(\widehat {xOy} = 70^\circ \). Tia Om là tia phân giác của \(\widehat {xOy}\), tia On là tia đối của tia Om. Tính số đo của \(\widehat {xOn}\)?
- Cho điểm A nằm ngoài đường thẳng p. Có bao nhiêu đt song song với d và đi qua A?
- Trong các phân số dưới đây, phân số nào biểu diễn số hữu tỉ \(0,0625\)?
- Kết quả của phép tính \({\left( {0,08} \right)^6}{.10^6}\) là?
- Hãy so sánh \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \)?
- Hãy chọn câu đúng trong các câu dưới?
- Cho góc bẹt \(xOy\). Vẽ tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\). Vẽ tia \(Om\) là phân giác của
- Cho hình vẽ, biết \(AE\,//\,BD,\,\angle ABD = {90^o},\,\angle AED = {55^o}.\) Số đo góc \(\angle BAE\) và
- Tìm phát biểu đúng trong các phát biểu sau?
- Tìm \(x\), biết: \(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)?
- Kết quả của phép tính sau đay \(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\) là?
- Cho hình bên dưới. Chọn câu đúng nhất?
- Vẽ hai đoạn thẳng \(AA',\,CC'\) cắt nhau tại \(B\) sao cho \(\angle A'BC = {47^o}.\) Số đo các góc \(\angle ABC',\,\angle ABC,\,\angle A'BC'\) bằng?
- Điền cụm từ còn thiếu vào …: “Định lí …”?
- Cách viết nào dưới đây biểu diễn số hữu tỉ?
- Khẳng định nào sau đây là đúng?
- Số đối của phân số \( - \frac{1}{2}\) là?
- Chọn khẳng định sai?
- Giá trị tuyệt đối của số - 0,7 là?
- Cho \(a;b \in \mathbb{R};\,a < b < 0\) khẳng định nào đúng?
- Hai góc vị trí kề bù có tổng số đo góc là?
- Cho hình sau, biết góc x’Oy’ = 300. Số đo của góc xOy là?
- Trong các số sau: Số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?
- Phát biểu định lý trong hình bằng lời?

