Đề minh họa ĐGNL 2025 môn Toán Trường Đại học Sư phạm HCM

BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM THÀNH PHỐ HỒ CHÍ MINH ĐỀ THI MINH HỌA (Đề thi có 12 trang)

ĐỀ THI ĐÁNH GIÁ NĂNG LỰC CHUYÊN BIỆT NĂM 2025 Môn thi: TOÁN Thời gian làm bài: 90 phút, không kể thời gian phát đề

Họ, tên thí sinh: ..............................................................................................................................................

Số báo danh: ..................................................................................................................................................

Thí sinh lựa chọn một phương án đúng theo yêu cầu từ câu 1 đến câu 20.

Câu 1: Cho hàm số \(y = f(x)\) có bảng xét dấu đạo hàm như sau:

Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

A. \((0;2)\).                 

Β. \((-\infty;-2)\).

C. \((-2;2)\).

D. \((-2;0)\).

Câu 2: Nồng độ của một chất hóa học trong máu sau t giờ kể từ lúc tiêm vào cơ thể người được tính bởi công thức \(C = \frac{3t^2 +t}{t+50}\). Nồng độ chất hóa học đó thay đổi thế nào khi t đủ lớn?

A. Nồng độ dần về không.

B. Nồng độ còn lại một nửa.

C. Nồng độ dần về giá trị 0,06.

D. Nồng độ ổn định với giá trị bằng 3.

Câu 3: Hàm số nào dưới đây là một nguyên hàm của hàm số \(f(x) = 3x^2 - \frac{2}{x}\)?

A. \(y = x^2 - 2 ln|x|\).

B. \(y = 6x-2ln|x|\).

C. \(y = x^3 + \frac{2}{x^2}\).

D. \(y = 6x+ \frac{2}{x^2}\).

Câu 4: Cho hàm số f(x) liên tục trên R thỏa mãn \(\int_{-1}^8 f(x)dx=-1\) và \(\int_{4}^8 f(x)dx = 4\). Giá trị của \(P = \int_{-1}^4 f(x)dx\) bằng bao nhiêu?

A.  P = 3.

B. P = -3.

C. P = -5.

D. P = 5.

Câu 5: Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;4;-5) trên trục Oy là điểm nào dưới đây?

A. M (3;0;-5).

Β. N (3;-4;-5).

C. P(0;4;0).

D. Q(3;0;0).

Câu 6: Trong không gian Oxyz, vectơ \(\overrightarrow{n} = (1;-1;1)\) KHÔNG là vectơ pháp tuyến của mặt phẳng nào dưới đây?

A. (P): 2x+y-z-3=0.

B. (Q):x-y+z-3=0.

C. \((R): \frac{x}{3} + \frac{y}{-3} + \frac{z}{3} =1\).

D. \((T):-(x-1)+(y+1)-(z-1)=0\).

Câu 7: Trong không gian Oxyz, cho mặt phẳng (P): 2x-3y-z-4 = 0. Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua điểm I (-1;0;2) và vuông góc với (P)?

A. \(\left\{ {\begin{array}{*{20}{l}}
{x = 1 - 2t}\\
{y = 3t}\\
{z = 2 + t}
\end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{l}}
{x =  - 1 + 2t}\\
{y =  - 3t}\\
{z = 2 - t}
\end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{l}}
{x = 2 + t}\\
{y =  - 3}\\
{z =  - 1 - 2t}
\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}}
{x = 2 - t}\\
{y =  - 3}\\
{z =  - 1 + 2t}
\end{array}} \right.\)

Câu 8: Trong không gian Oxyz, cho mặt cầu \((S):{{(x+1)}^{\text{2}}}+{{(y+2)}^{2}}+{{(z-1)}^{\text{2}}}=3\). Tâm của (S) là điểm nào dưới đây?

A. M (-1;-2;-1).

Β. N(-1;-2;1).

C. P(1;2;-1).

D. Q(1;2;1).

Câu 9: Bảng dưới đây thống kê kết quả điểm khảo sát môn Tiếng Anh của học sinh khối 12 trong một trường A:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng bao nhiêu?

A. 90.

B. 100.

C. 110.

D. 152.

Câu 10: Cho hai biến cố A và B, trong đó \)P(A) > 0\). Xác suất của biến cố B với điều kiện A bằng biểu thức nào dưới đây?

A. \(\frac{P(A\cap B)}{P(A)}.\)

B. \(\frac{P(A\cap B)}{P(B)}.\)

C. \(\frac{P(A)}{P(A\cap B)}.\)

D. \(\frac{P(B)}{P(A)}.\)

Câu 11: Cho hàm số \(y=2{{x}^{\text{2}}}-1\). Phương án nào dưới đây đúng?

A. \({y}'=(2x-1){{2}^{2{{x}^{\text{2}}}-1}}\ln 2\).

B. \({y}'=2x{{2}^{2{{x}^{\text{2}}}-1}}\ln 2\).

C. \({y}'=2{{x}^{2{{x}^{\text{2}}}-1}}\ln 2\).

D. \({y}'=(2x-1){{2}^{2{{x}^{\text{2}}}-1}}\).

Câu 12: Cho a > 0 và \(a \neq 1\). Giá trị \(log_a \sqrt{a}\) bằng bao nhiêu?

A. 2.

B. -2.

C. \(\frac{1}{2}\).

D. \(\frac{1}{2}\).

Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và cạnh SA vuông góc với mặt phẳng đáy. Góc giữa hai đường thẳng SB và AD bằng bao nhiêu?

A. \(60^\circ\).

B. \(45^\circ\).

C. \(90^\circ\).

D. \(30^\circ\).

Câu 14: Cho khối hộp chữ nhật ABCD.A'B'C'D'có AA' = a, AB = a, \(AD = a \sqrt{2}\). Góc giữa đường thẳng A'C và mặt phẳng (ABCD) bằng bao nhiêu?

A. \(60^\circ\).

B. \(45^\circ\).

C. \(90^\circ\).

D. \(30^\circ\).

Câu 15: Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng đáy (ABC), tam giác ABC vuông tại B. Phương án nào dưới đây SAI?

A. (SAB) vuông góc với (ABC).

B. (SAC) vuông góc với (ABC).

C. (SAB) vuông góc với (SBC).

D. (SBC) vuông góc với (ABC).

Câu 16: Cho \(F(x) = 3x^2 +1\) và \(G(x)=4x^2+2x\) lần lượt là nguyên hàm của f(x) và g(x). Xét H (x) là một nguyên hàm của hàm số h(x) = f(x)g(x). Phương án nào dưới đây đúng?

A. \(H(x) = (3x^2+1)(4x^2+2x)\).

B. \(H(x)=(x^2+x)(x^2+x^2)\).

C. \(H(x) = 6x(12x^2 +2)\).

D. \(H(x)= 6(x^2-1)(3x^2+4)\).

Câu 17: Một bệnh viện thống kê chiều cao của 50 trẻ sơ sinh 12 ngày tuổi một cách ngẫu nhiên. Kết quả thu được như sau :

Bộ giá trị nào sau đây là tứ phân vị của mẫu số liệu ghép nhóm trên?

A. \(Q_1 = 45; Q_2 = 47; Q_3 = 51\).

B. \(Q_1 = 45,5; Q_2 = 47,5; Q_3 = 51,5\).

C. \(Q_1 = 45,3; Q_2 = 48,3; Q_3 = 53,3\).

D. \(Q_1 = 45,8; Q_2 = 48,3; Q_3 = 50,1\).

Câu 18: Cho khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông, BD = 2, góc giữa hai mặt phẳng (A'BD) và (ABCD) bằng \(60^\circ\). Thể tích của khối lăng trụ đứng đã cho bằng bao nhiêu?

A. \(\frac{2\sqrt{3}}{9}\).

B. \(6\sqrt{3}\).

C. \(\frac{2\sqrt{3}}{3}\).

D. \(2\sqrt{3}\).

Câu 19: Biết rằng có 0,5% dân số nhiễm virus X. Ông A muốn biết mình có bị nhiễm virus X hay không nên đã đến một bệnh viện để thực hiện một xét nghiệm phát hiện virus. Cho biết xét nghiệm này có sai số là 1% (tức là nếu ông A thực sự bị nhiễm virus X thì xác suất ông A nhận kết quả không bị nhiễm là 1%; ngược lại, nếu ông A thực sự không bị nhiễm virus X thì xác suất ông A nhận kết quả bị nhiễm là 1%). Xác suất ông A nhận kết quả bị nhiễm virus X từ xét nghiệm này là bao nhiêu?

A. 0,005.

B. 0,01.

C. 0,0149.

D. 0,0198.

Câu 20: Cho khối chóp cụt tứ giác đều có các cạnh đáy lần lượt bằng 6 và 8, chiều cao của mặt bên bằng 5. Thể tích của khối chóp cụt đã cho bằng bao nhiêu?

A. \(\frac{148\sqrt{26}}{3}\)

B. \(\frac{740}{3}\)

C. \(\frac{296\sqrt{6}}{3}\)

D. \(\frac{148\sqrt{21}}{3}\)

Thí sinh chọn các phương án đúng theo yêu cầu từ câu 21 đến câu 25 (nếu chọn duy nhất một phương án mà phương án đó là phương án đúng sẽ được tính một nửa số điểm của câu hỏi. Nếu chọn tất cả các phương án đúng sẽ đạt điểm tối đa của câu hỏi).

Câu 21: Trên trục Os, cho hai chất điểm chuyển động có tọa độ theo thời gian t (giây) lần lượt là s₁ = 2sint và s₂ = sin 2t (tham khảo hình vẽ minh họa).

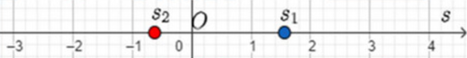
Những phương án nào dưới đây đúng?

1. Trong 4 giây đầu tiên, khoảng cách giữa hai chất điểm lớn nhất là 2,60 (làm tròn đến hàng phần trăm)

2. Trong 2 giây đầu tiên, khi s₁ lớn nhất thì sẽ bằng 0.

3. Trong 2 giây đầu tiên, khi sĩ lớn nhất thì sĩ bằng 2.

4. Trong 4 giây đầu tiên, s₁ và sẽ bằng nhau tại 4 thời điểm.

Câu 22: Trong không gian Oxyz, xét đường thẳng A đi qua M (2;-1;1) và cắt cả hai đường thẳng d₁: \(\frac{x-2}{-2} = \frac{y-1}{-2}=\frac{z-1}{2}\), d₂: \(\frac{x-2}{2} = \frac{y+3}{1}=\frac{z-1}{-1}\). Những phương án nào dưới đây đúng?

1. Đường thẳng A có một vectơ chỉ phương là \(\overrightarrow{u}\) = (0;1;1).

2. Phương trình tham số của A là \(\begin{cases} x=2 \\ y=1+t. \\ z=1 \end{cases}\)

3. Đường thẳng A cắt mặt phẳng (Ozx) tại điểm A(2;0;1).

4. Đường thẳng A vuông góc với đường thẳng d: \(\frac{x-2}{2} = \frac{y}{1}=\frac{z+1}{-1}\)

Câu 23: Có hai hộp đựng câu hỏi thi (phiếu), mỗi phiếu ghi một câu hỏi. Hộp thứ nhất có 15 phiếu và hộp thứ hai có 9 phiếu. Biết rằng sinh viên A đi thi chỉ thuộc 10 câu ở hộp thứ nhất và 8 câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên từ mỗi hộp ra một phiếu thi, sau đó cho sinh viên A rút ngẫu nhiên ra 1 phiếu từ 2 phiếu mà thầy giáo đã rút. Gọi \(E_1\) là biến cố sinh viên A rút ra phiếu từ hộp thứ nhất, \(E_2\) là biến cố sinh viên A rút ra phiếu từ hộp thứ hai. Những phương án nào dưới đây đúng?

1. Xác suất của biến cố \(E_1\) bằng \(\frac{1}{2}\).

2. Gọi B là biến cố sinh viên A rút được phiếu đã học thuộc thì \(B = (B\cap E_1)(B\cap E_2)\).

3. Xác suất có điều kiện \(P(B|E_1) = \frac{8}{9}\).

4. Nếu sinh viên A rút được phiếu đã học thuộc thì xác suất phiếu đó thuộc hộp thứ nhất bằng \(\frac{3}{7}\).

Câu 24: Xét phương trình \(\log(x+\sqrt{x^2+1}) = \frac{3}{a}(\frac{x}{2})^b\) trên khoảng (-2;2), với a và b là hai số nguyên dương đều bé hơn 20. Những phương án nào dưới đây đúng?

1. Nếu b chẵn thì phương trình có nhiều nhất 2 nghiệm phân biệt trên khoảng (-2;2).

2. Nếu b lẻ thì phương trình có nhiều nhất 1 nghiệm trên khoảng (-2;2).

3. Có 38 cặp (a,b) sao cho phương trình có đúng 3 nghiệm phân biệt trên khoảng (-2;2).

4. Nếu a = 1 thì có đúng 9 giá trị của b sao cho phương trình có đúng 3 nghiệm phân biệt trên khoảng (-2;2).

5. Nếu a = 3 thì có đúng 10 giá trị của b sao cho phương trình có đúng 3 nghiệm phân biệt trên khoảng (-2;2).

Câu 25: Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, cạnh AB = 1, cạnh SA vuông góc với mặt phẳng đáy (ABC) và \(SA = \sqrt{2}\). Gọi M là trung điểm của BC. Những phương án nào dưới đây đúng?

1. Khoảng cách giữa hai đường thẳng AC và SM bằng \(\frac{\sqrt{2}}{3}\).

2. Khoảng cách giữa hai đường thẳng AM và SB bằng \(\frac{\sqrt{10}}{5}\).

3. Khoảng cách giữa hai đường thẳng SA và BC bằng \(\frac{\sqrt{2}}{3}\).

4. Khoảng cách giữa hai đường thẳng SB và AC bằng \(\frac{\sqrt{6}}{4}\).

5. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{\sqrt{10}}{4}\).

Dựa vào thông tin dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu từ câu 26 đến câu 28.

Một cái thùng hình trụ không có nắp, bên trong thùng có chứa một lượng nước. Một cái nút chai nhấp nhô lên xuống trong thùng (xem Hình 1), biết rằng khoảng cách từ tâm nút chai đến đáy thùng được cho bởi công thức s(t) = 50+ cos(t) cm, theo thời gian t giây (t≥0).

Hình 1

Câu 26: Nút chai gần với đáy nhất tại thời điểm nào dưới đây?

A. t = 1 giây.

B. t = 2 giây.

C. t = 0,5 giây.

D. t = 1,5 giây.

Câu 27: Thứ tự thời gian (tính bằng đơn vị giây) nào sau đây có vận tốc tức thời tương ứng của nút chai giảm dần?

A. \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{2}\).

B. \(\frac{3}{2}\), \(\frac{1}{4}\), \(\frac{1}{2}\).

C. \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{2}\).

D. \(\frac{3}{2}\), \(\frac{1}{2}\), \(\frac{1}{4}\).

Câu 28: Ông A định làm một cái thùng hình trụ không nắp như trên bằng kim loại có thể tích cho trước. Để giảm thiểu lượng kim loại được sử dụng, ông A cần làm cái thùng sao cho diện tích bề mặt phải càng nhỏ càng tốt (Hình 2). Chiều cao của thùng bằng bao nhiêu lần bán kính đáy thì tiết kiệm kim loại nhất?

Hình 2

A. 1.

B. 2.

C. \(\frac{1}{2}\).

D. π.

Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu 29 và câu 30.

Ông B muốn tạo ra một lọ hoa mới với hình dạng đặc biệt, trong đó phần thân lọ từ đáy đến miệng lọ được tạo thành bằng cách quay đường cong \(y = \frac{1}{2} + ln(x+1)\) quanh trục Ox từ x=0 đến x = e-1.

Câu 29: Đường kính lớn nhất của lọ hoa bằng bao nhiêu?

A. \(\frac{3}{2}\).

B. \(e-1\).

C. \(3\pi\).

D. 3.

Câu 30: Thể tích của lọ hoa xấp xỉ bằng bao nhiêu?

A. 2,1479.

B. 6,7477.

C. 5,8407.

D. 13,4954.

Thí sinh điền đáp án vào ô trống theo yêu cầu từ câu 31 đến câu 40.

Câu 31: Xét hình phẳng giới hạn bởi hai parabol \(y = x^2-c^2\) và \(y = c^2-x^2\). Tìm hằng số dương c sao cho diện tích hình phẳng đó bằng 10 (làm tròn kết quả đến hàng phần trăm).

Đáp án:

Câu 32: Trong không gian Oxyz, cho mặt phẳng (P): \(ax + by + cz+9=0\) chứa hai điểm A(3;2;1), B(-3;5;2) và vuông góc với mặt phẳng (Q): \(3x+y+z-5=0\). Tính tổng S = a+b+c.

Đáp án:

Câu 33: Theo nhận định từ các chuyên gia, khả năng công ty của ông A mở một chi nhánh mới ở thành phố X là 40% có thể xảy ra. Nếu đúng như vậy thì khả năng ông A được bổ nhiệm làm giám đốc cho chi nhánh mới này là 80% có thể xảy ra. Xác suất để ông A trở thành giám đốc cho chi nhánh ở thành phố X là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.

Đáp án:

Câu 34: Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình dưới đây. Biết f(-1) = -2.

Gọi S là tập hợp các giá trị m nguyên bé hơn 100 để bất phương trình \(f(x)-\frac{5}{3}x^3

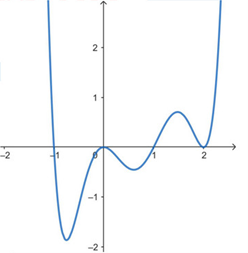
Đáp án:

Câu 35: Số lượng cá tính từ lúc thả trong một cái ao sau thời gian  t (tính bằng tháng) được cho bởi công thức \(P(t)=\frac{1000}{1+9e^{-t}}\). Sau n tháng (n là số tự nhiên) thì số lượng cá trong ao vượt hơn 500 con. Số n nhỏ nhất là bao nhiêu?

Đáp án

Câu 36: Một người chèo một chiếc thuyền xuất phát từ điểm A trên bờ một con sông thẳng rộng 2km, và muốn đến điểm B cách bờ đối diện 10km. Người này có thể chỉ chèo thuyền hoặc kết hợp chèo thuyền với chạy bộ, càng nhanh càng tốt. Chẳng hạn, anh ta có thể chèo thuyền qua sông đến điểm C rồi chạy bộ đến điểm B, hoặc anh ta có thể chèo thuyền thẳng đến B, hoặc anh ta có thể chèo thuyền đến một điểm D nào đó ở giữa C và B rồi chạy bộ đến B, xem hình vẽ minh họa dưới đây. Biết rằng vận tốc chèo thuyền của anh ta là 6km/h (đã tính vận tốc dòng nước), vận tốc chạy bộ của anh ta là 10km/h. Trong tất cả các phương án đến B bằng cách chèo thuyền hoặc chèo thuyền rồi chạy bộ, phương án nhanh nhất có tổng thời gian là bao nhiêu giờ? Làm tròn kết quả đến hàng phần trăm.

Đáp án:

Câu 37: Cho f(x) là hàm số bậc hai thỏa mãn \(f(0) = 1 = 1\) và \(\int \frac{f(x)}{x^2(x+1)^3} dx\)là một họ hàm số

có dạng \(\frac{P(x)}{Q(x)}\), trong đó P(x), Q(x) là các đa thức. Tính f'(0).

Đáp án:

Câu 38: Trong không gian Oxyz, cho hai điểm A(1;0;1), B(-1;1;0) và điểm C nằm trên tia Ox. Biết rằng đường phân giác trong xuất phát từ A vuông góc với đường trung tuyến xuất phát từ B của tam giác ABC. Tìm hoành độ của điểm C. Làm tròn kết quả đến hàng phần trăm.

Đáp án:

Câu 39: Trong không gian Oxyz, cho ba điểm A(2;3;3), B(0;5;5), C(1;1;1). Gọi (P) là mặt phẳng đi qua C sao cho (P) cách A một đoạn bằng 3 và cách B một đoạn bằng 5. Tính khoảng cách từ O đến (P). Làm tròn kết quả đến hàng phần trăm.

Đáp án:

Câu 40: Trong không gian Oxyz, cho đường tròn (C) là giao tuyến của mặt cầu \((S):x^2 + y^2 + z^2 = 4\) và mặt phẳng (P): 2x+y-2z-3=0. Xét mặt cầu (T) đi qua (C) và tiếp xúc mặt phẳng (Q): 2x+y-2z+1 = 0. Tính bán kính của (T). Làm tròn kết quả đến hàng phần trăm.

Đáp án:

Câu hỏi	1	2	3	4	5	6	7	8	9	10
Đáp án	D	A	A	C	C	A	B	B	A	A
Câu hỏi	11	12	13	14	15	16	17	18	19	20
Đáp án	B	D	C	D	D	D	D	D	C	C
Câu hỏi	21	22	23	24	25	26	27	28	29	30
Đáp án	1 và 2	3	1	1 và 4	1 và 2	A	B	A	D	B
Câu hỏi	31	32	33	34	35	36	37	38	39	40
Đáp án	1,55	4	0,32	4949	3	1,27	3	5,80	1,67	1,79

 

Trên đây là một phần nội dung tài liệu Đề minh hoạ ĐGNL 2025 môn Toán Trường Đại học Sư phạm TPHCM. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Mời các em tham khảo các tài liệu có liên quan:

• Đề thi minh họa ĐGNL 2025 môn Vật lí Trường Đại học Sư phạm HCM
• Đề minh hoạ ĐGNL 2025 môn Ngữ văn Trường Đại học Sư phạm TP.HCM

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.