Phương trình bậc hai một ẩn là một chương rất quan trọng ở chương trình toán lớp 9 cũng như áp dụng của nó vào thực tiễn và đời sống. Ngoài ra còn là kiến thức nền tảng để các em có thêm kiến thức học tốt toán cấp 3
Tóm tắt lý thuyết
Kiến thức cần nhớ
1. Đồ thị hàm số \(y=ax^2 (a\neq 0)\)
Đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.
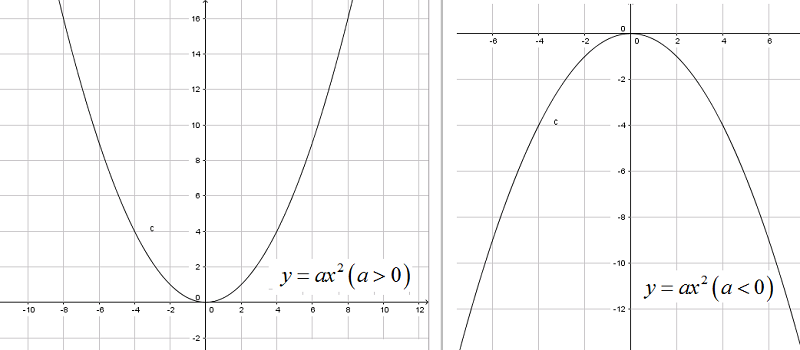
2. Phương trình bậc hai
Phương trình bậc hai một ẩn (gọi tắt là phương trình bậc hai) là phương trình có dạng \(ax^2+bx+c=0\)
Trong đó, x là ẩn; các hệ số a, b, c là các số cho trước và \(a\neq 0\)
3. Công thức nghiệm của phương trình bậc hai
Với phương trình \(ax^2+bx+c=0 (a\neq 0)\) và biệt thức \(\Delta =b^2-4ac\):
\(\Delta>0\) thì phương trình có 2 nghiệm phân biệt:
\(x_{1}=\frac{-b+\sqrt{\Delta }}{2a}\); \(x_{2}=\frac{-b-\sqrt{\Delta }}{2a}\)
\(\Delta=0\) thì phương trình có nghiệm kép \(x=x_{1}=x_{2}=-\frac{b}{2a}\)
\(\Delta<0\) phương trình vô nghiệm.
4. Công thức nghiệm thu gọn
Với các phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) và \(b=2b'\), \(\Delta '=b'^2-ac\) thì:
Nếu \(\Delta '>0\) thì phương trình có hai nghiệm phân biệt
\(x_{1}=\frac{-b'+\sqrt{\Delta '}}{a}; x_{2}=\frac{-b'-\sqrt{\Delta '}}{a}\)
Nếu \(\Delta '=0\) thì phương trình có nghiệm kép \(x=\frac{-b'}{a}\)
Nếu \(\Delta '<0\) thì phương trình vô nghiệm.
5. Định lí Vi ét và ứng dụng
Phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) có 2 nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\Delta }}{2a}; x_2=\frac{-b-\sqrt{\Delta }}{2a}\)
Ta có: \(x_1+x_2=\frac{-2b+\sqrt{\Delta }-\sqrt{\Delta }}{2a}=-\frac{b}{a}\)
\(x_1.x_2=\frac{b^2-\Delta }{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)
Định lý Vi-ét
Nếu \(x_1;x_2\) là hai nghiệm của phương trình \(ax^2+bx+c=0 (a\neq 0)\) thì:
\(x_1+x_2=-\frac{b}{a}\)
và \(x_1.x_2=\frac{c}{a}\)
Tổng quát
Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a+b+c=0\) thì phương trình có một nghiệm là \(x_1=1\) và nghiệm kia là \(x_2=\frac{c}{a}\).
Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a-b+c=0\) thì phương trình có một nghiệm là \(x_1=-1\) và nghiệm kia là \(x_2=-\frac{c}{a}\).
6. Các phương trình quy về phương trình bậc hai (phương trình trùng phương, phương trình có ẩn ở mẫu, phương trình tích...)
a. Phương trình trùng phương
Định nghĩa
Phương trình trùng phương là phương trình có dạng: \(ax^4+bx^2+c=0 (a\neq 0)\)
b. Phương trình chứa ẩn ở mẫu
Các bước để giải phương trình chứa ẩn ở mẫu đã học ở lớp 8
Bước 1: Tìm điều kiện xác định của phương trình
Bước 2: Quy đồng hai vế rồi khử mẫu
Bước 3: Giải phương trình vừa nhận được
Bước 4: So sánh điều kiện ban đầu rồi kết luận nghiệm
c. Phương trình tích
Nhắc lại kiến thức đã học ở lớp dưới:
Biến đổi phương trình về dạng \(A.B.C.....=0\) rồi suy ra hoặc \(A=0\) hoặc \(B=0\) hoặc.....
7. Giải toán bằng phương pháp lập phương trình
Phương pháp giải
Để giải bài toán bằng cách lập phương trình, chúng ta làm theo các bước sau:
Bước 1: Lập phương trình
Chọn ẩn và đặt điều kiện cho ẩn
Biểu đạt các đại lượng khác nhau theo ẩn
Dựa vào đề bài toán, lập phương trình theo dạng đã học
Bước 2: Giải phương trình
Bước 3: So sánh kết quả tìm được và chọn nghiệm thích hợp
Bài tập minh họa
Các bài tập trọng tâm
Bài 1: Giải phương trình bằng cách phân tích đa thức thành nhân tử: \(x^2-11x-12=0\)
Hướng dẫn:\(x^2-11x-12=0\)
\(\Leftrightarrow x^2-12x+x-12=0\)
\(\Leftrightarrow x(x-12)+x-12=0\)
\(\Leftrightarrow (x+1)(x-12)=0\)
Vậy phương trình trên có hai nghiệm phân biệt là \(x=-1;x=12\)
Bài 2:
Giải phương trình: \(x^2+10x+25=0\); \(x^2-4x-9=0\)
Hướng dẫn: \(x^2+10x+25=0\)
Giải: \(\Delta =10^2-4.1.25=0\) \(\Rightarrow x=\frac{-0}{2}=-5\)
\(x^2-4x-9=0\)
Giải: \(\Delta =(-4)^2-4.1.(-9)=52\Rightarrow \sqrt{\Delta }=2\sqrt{13}>0\)
\(\Rightarrow x_{1}=\frac{-(-4)+2\sqrt{13}}{2}=2+\sqrt{13};x_{2}=\frac{-(-4)-2\sqrt{13}}{2}=2-\sqrt{13}\)
Bài 3:
Tìm hai số biết hiệu của chúng là 5 và tích của chúng là 150
Hướng dẫn: Gọi hai số cần tim là a, b
Ta có \(\left\{\begin{matrix} a-b=5\\ ab=150 \end{matrix}\right.\)
Thế \(a=5+b\) vào phương trình tích, ta được \(b(b+5)=150\Leftrightarrow b^2+5b-150=0\)
\(\Rightarrow b=-15\) hoặc \(b=10\)
\(b=-15\Rightarrow a=-10\)
\(b=10\Rightarrow a=15\)
Bài 4:
Giải phương trình trùng phương sau: \(x^4-4x^2-5=0\)
Hướng dẫn: Đặt \(t=x^2 (t\geq 0)\)
Khi đó, phương trình trở thành: \(t^2-4t-5=0\)
Giải phương trình bậc hai cơ bản trên, ta được:
\(t=-1\) (loại)
\(t=5\) (nhận)\(\Rightarrow x=\pm \sqrt{5}\)
Lời kết
Để cũng cố bài học, xin mời các em cũng làm bài kiểm tra Trắc nghiệm Toán 9 Chương 4 Bài 9 với những câu hỏi củng cố bám sát nội dung bài học. Bên cạnh đó các em có thể nêu thắc mắc của mình thông qua phần Hỏi đáp Toán 9 Chương 4 Bài 9 cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 9 Chương 4 Bài 9 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9
-- Mod Toán Học 9 HỌC247













