Bài tập 9.2 tr 111 sách BT Toán lớp 9 Tập 2
Tính chu vi của hình cánh hoa, biết \(OA = R\) \((h.bs.6).\)
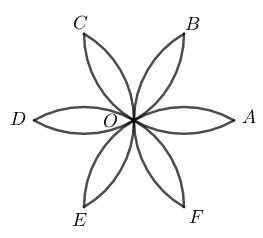
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Trong đường tròn \(R,\) độ dài \(l\) của một cung \(n^\circ\) được tính theo công thức: \(l=\dfrac{\pi Rn}{180}.\)
Lời giải chi tiết
Hình vẽ có 6 cung tròn bằng nhau có bán kính bằng R
\(\overparen{BOF}\) của đường tròn (A; R)
\(\overparen{AOC}\) của đường tròn (B; R)
\(\overparen{BOD}\) của đường tròn (C; R)
\(\overparen{COE}\) của đường tròn (D; R)
\(\overparen{DOF}\) của đường tròn (E; R)
\(\overparen{EOA}\) của đường tròn (F; R)
.jpg)
∆AOB đều, ∆AOF đều nên \(\widehat {BAF} = {120^0}\)
\( \Rightarrow \) sđ \(\overparen{BOF}\)= 1200
\(l = {{\pi R.120} \over {180}} = {{2\pi R} \over 3}\)
Chu vi cánh hoa: \({{2\pi R} \over 3}.6 = 4\pi R\)
-- Mod Toán 9 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





