Bài tập 29 trang 105 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

+) Số đo của nửa đường tròn bằng \(180^o.\)

+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

Lời giải chi tiết

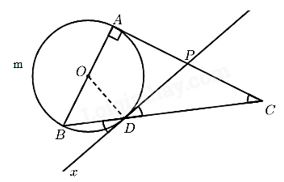
Trong đường tròn \((O)\) ta có \(\widehat C\) là góc có đỉnh ở ngoài đường tròn. 

\(\widehat C =\displaystyle{1 \over 2} (sđ \overparen{AmB}\) - sđ \(\overparen{AD}\)) (tính chất góc có đỉnh ở ngoài đường tròn)

 mà \(sđ \overparen{AmB} = sđ \overparen{ADB}=180^o\) 

\(\widehat C =\displaystyle {1 \over 2} (sđ \overparen{ADB}\) - sđ \(\overparen{AD}\)) \(= \displaystyle{1 \over 2} (sđ \overparen{AD}\) + sđ \(\overparen{DB}\) - sđ \(\overparen{AD}\))\(= \displaystyle {1 \over 2} sđ \overparen{BD}\)     \( (1)\)

\(\widehat {CDP} = \widehat {BDx}\) (đối đỉnh) \( (2)\) 

\(\widehat {BDx} =\displaystyle {1 \over 2} sđ \overparen{BD}\) (góc giữa tia tiếp tuyến và dây cung)   \((3)\)

Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat C = \widehat {CDP} \Rightarrow \Delta PCD\) cân tại \(P.\)

Vậy \(PD = PC\)

-- Mod Toán 9 HỌC247