Bài tập 7 trang 76 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

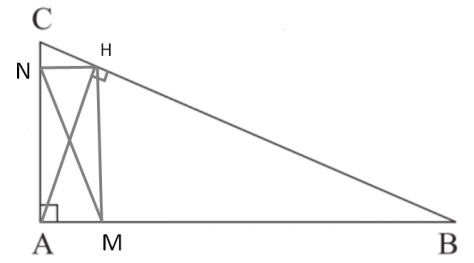
a) Xét tam giác vuông AMH và AHB ta có: \(\widehat{A}\) chung

Suy ra ΔAMH ᔕ ΔAHB (g.g)

b) ΔAMH ᔕ ΔAHB nên \(\frac{AM}{AH}=\frac{AH}{AB}\) hay \(AM.AB=AH^{2}\) (1)

Xét tam giác vuông ANH và AHC ta có: \(\widehat{A}\) chung

Suy ra ΔANH ᔕ ΔAHC (g.g)

Nên \(\frac{AN}{AH}=\frac{AH}{AC}\) hay \(AN.AC=AH^{2}\) (2)

Từ (1) và (2) suy ra AM.AB = AN.AC

c) Ta có AM.AB = AN.AC, do đó \(\frac{AN}{AB}=\frac{AM}{AC}\)

Xét tam giác vuông AMN và ABC ta có:

\(\frac{AN}{AB}=\frac{AM}{AC}\)

Suy ra ΔANM ᔕ ΔABC (c.g.c)

d) Áp dụng định lí Pythagore cho tam giác ABC ta có:

\(BC^{2}=AB^{2}+AC^{2} \Rightarrow BC = 15\) (cm)

Ta có \(AH.BC = AB.AC \Rightarrow AH.15 = 9.12 \Rightarrow AH = 7,2\) (cm)

Xét tứ giác AMHN có bốn góc vuông nên AMHN là hình chữ nhật.

\(\Rightarrow AH = MN = 7,2\) (cm)

Vậy ΔAMN ᔕ ΔABC theo tỉ số đồng dạng \(k=\frac{MN}{BC}=\frac{7,2}{15}=\frac{12}{25}\)

Nên tỉ số diện tích của tam giác AMN và ABC là \(k^{2}=\frac{144}{625}\)

Diện tích tam giác ABC là: \(\frac{1}{2}AB.AC=54 (cm^{2})\)

Diện tích tam giác AMN là: \(54.\frac{144}{625}=12,4416(cm^{2})\)

Vậy diện tích tam giác AMN: \(12,4416(cm^{2})\)

-- Mod Toán 8 HỌC247