Bài tập 6.3 trang 165 SBT Toán 8 Tập 1
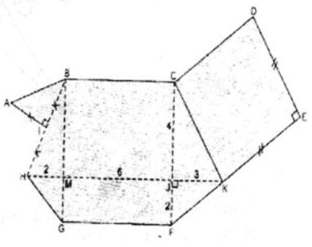
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.
Hướng dẫn giải chi tiết
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB
Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)
⇒ BC = GF = MJ = 6 (cm)
CJ = CF – FG = 6 – 2 = 4 (cm)
SKFGH = \(\frac{{HK + GF}}{2}.FJ\) = \(\frac{{11 + 6}}{2}.2\) = 17 (cm2)
SBCKH = \(\frac{{BC + KH}}{2}.FJ\) = \(\frac{{11 + 6}}{2}.4\) = 34 (cm2)
Trong tam giác vuông BMH có \(\widehat J = {90^0}\) .Theo định lý Pi-ta-go ta có:
CK2= CJ2 + JK2 = 16 + 9 = 25 ⇒ CK = 5 (cm)
SCDEK = CK2 = 52 = 25 (cm2)
Trong tam giác vuông BMH có \(\widehat M = {90^0}\) .Theo định lý Pi-ta-go ta có:
BH2= BM2 + HM2
mà BM = CJ = 4(cm) (đường cao hình thang BCKH)
⇒ BH2 = 42 + 22 = 20
IB = \(\frac{{BH}}{2}\) ⇒ IB2= \(\frac{{B{H^2}}}{4}\) = \(\frac{{20}}{4}\) = 5
IB = \(\sqrt 5 \) (cm)
ΔAIB vuông cân tại I (vì AI = IH = IB)
SAIB = \(\frac{{1}}{2}\) AI. IB = \(\frac{{1}}{2}\) IB2 = \(\frac{{5}}{2}\) (cm2)
S = SCDEK + SKFGH + SBCKH + SAIB = 25 + 17 + 34 + \(\frac{{5}}{2}\) = \(\frac{{157}}{2}\) (cm2)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 6.1 trang 164 SBT Toán 8 Tập 1
Bài tập 6.2 trang 165 SBT Toán 8 Tập 1
Bài tập 47 trang 164 SBT Toán 8 Tập 1
Bài tập 48 trang 164 SBT Toán 8 Tập 1
Bài tập 49 trang 164 SBT Toán 8 Tập 1
Bài tập 50 trang 164 SBT Toán 8 Tập 1
Bài tập 6.1 trang 164 SBT Toán 8 Tập 1
-


Bài 48 trang 164 sách bài tập toán 8
bởi Long lanh
 30/12/2019
Bài 48 (Sách bài tập - trang 164)
30/12/2019
Bài 48 (Sách bài tập - trang 164)Theo bản đồ và tỉ lệ ghi trên hình 190, hãy tính diện tích của hồ nước (phần gạch sọc) ?
Theo dõi (0) 1 Trả lời -


Bài 47 trang 164 sách bài tập toán 8 tập 1
bởi Lê Nhi
 29/09/2018
Bài 47 (Sách bài tập - trang 164)
29/09/2018
Bài 47 (Sách bài tập - trang 164)Thực hiện các phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE (BE // CD) (h.189) ?
Theo dõi (0) 1 Trả lời