Giải bài 6.1 tr 164 sách BT Toán lớp 8 Tập 1
Tính diện tích của hình được cho trong mỗi trường hợp sau đây:
a. Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs. 24
b. Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)
Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Hướng dẫn giải chi tiết
Hướng dẫn giải
Chia đa giác đã cho thành các hình thang và tam giác.
Dựa vào công thức diện tích tam giác và hình thang tính được diện tích của mỗi hình đó.
Áp dụng công thức tính diện tích hình tam giác bằng nửa tích cạnh và chiều cao tương ứng: \(S=\dfrac{1}{2}ab\) và công thức tính diện tích hình thang bằng nửa tích hai đáy với chiều cao: \(S=\dfrac{a+b}{2}.h\)
Sau đó suy ra được diện tích của đa giác đã cho.
Lời giải chi tiết
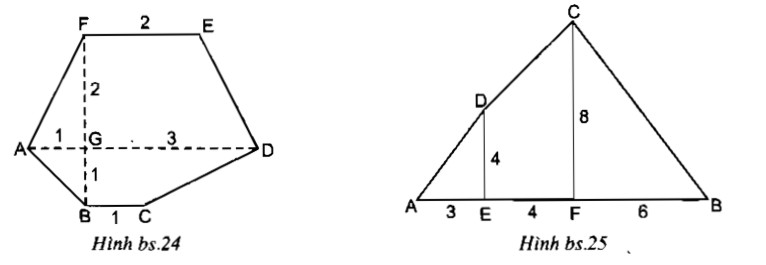
Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.
Hình thang ABCD có cạnh đáy BC = 1 (cm)
Đáy AD = AG + GD = 1 + 3 = 4 (cm)
Đường cao BG = 1 (cm)
\({S_{ABCD}} = {{AD + BC} \over 2}.FG = {{4 + 1} \over 2} = {5 \over 2}\) (cm2)
Hình thang ADEF có đáy AD = 4 (cm)
Đáy EF = 2cm, đường cao FG = 2cm
\(\eqalign{ & {S_{ADEF}} = {{AD + EF} \over 2}.FG = {{4 + 2} \over 2}.2 = 6(c{m^2}) \cr & {S_{ABCDEF}} = {S_{ABCD}} + {S_{ADEF}} = {5 \over 2} + 6 = {{17} \over 2}(c{m^2}) \cr} \)
b. Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
\(\eqalign{ & {S_{AED}} = {1 \over 2}AE.DE = {1 \over 2}.3.4 = 6(c{m^2}) \cr & {S_{EDCF}} = {{ED + FC} \over 2}{\rm{.EF = }}{{4 + 8} \over 2}.4 = 24(c{m^2}) \cr & {S_{CFB}} = {1 \over 2}CF.FB = {1 \over 2}.8.6 = 24(c{m^2}) \cr & {S_{ABCD}} = {S_{AED}} + {S_{EDCF}} + {S_{CFB}} = 6 + 24 + 24 = 54(c{m^2}) \cr} \)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.



